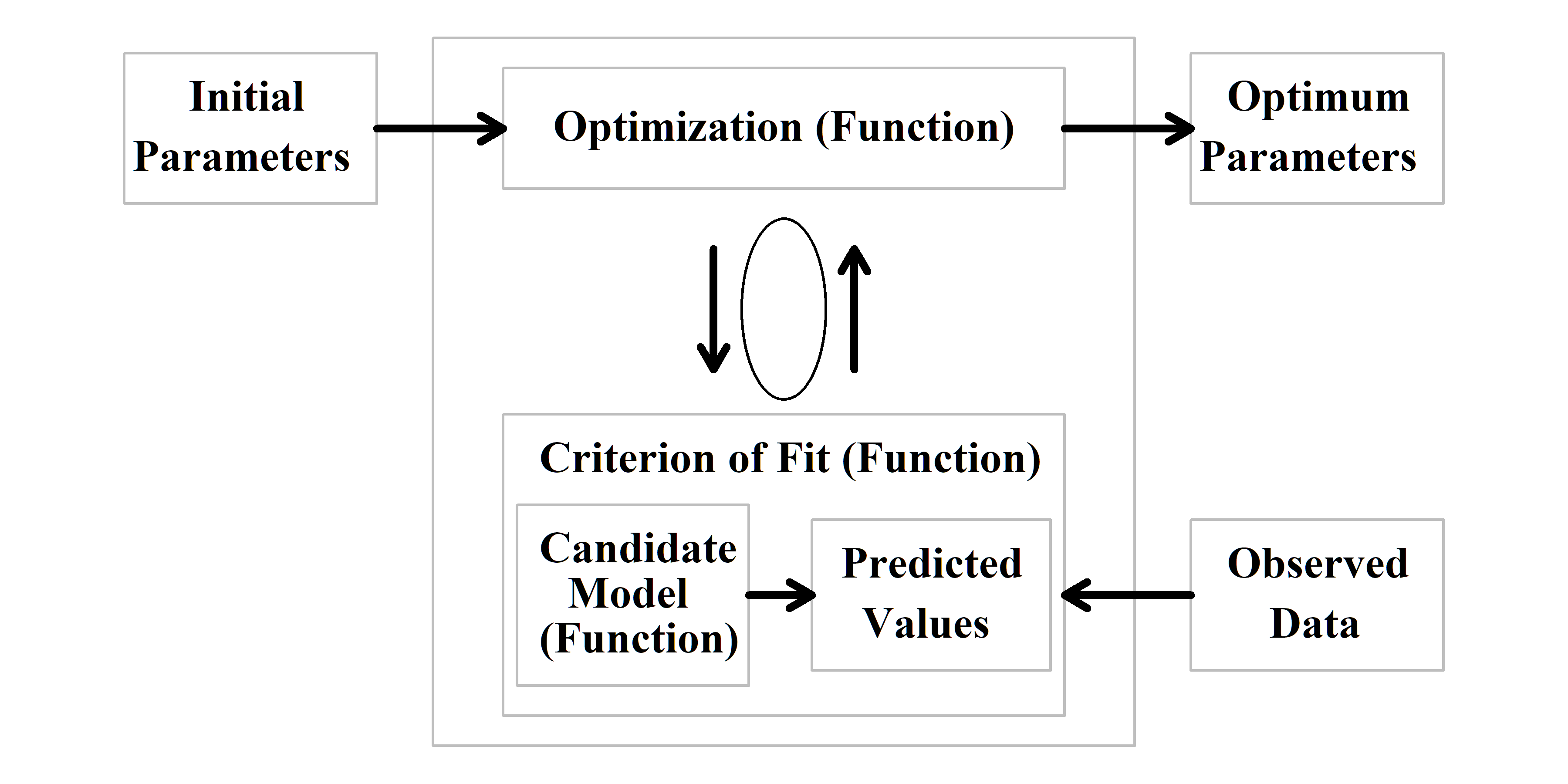
4 模型参数估算
4.1 引言
生态学和渔业学学建模的一个更重要的方面涉及到模型与数据的拟合。这种模型拟合需要:
从对自然感兴趣的过程中获得的数据(样本、观测),
明确地选择一个适合手头任务的模型结构(模型设计,然后选择——大的主题本身),
明确地选择概率密度函数来表示当比较时,模拟过程的预测将如何不同于自然观测的预期分布(选择残差结构) ,最后,
寻找模型参数,优化之间的预测模型和任何观测数据(模型拟合的准则)匹配。
在上面的最后一个需求中,将模型与数据相匹配时所涉及的许多技巧/诡计/魔术都集中在那个看起来无害的单词或概念上进行优化。这是一个几乎是恶作剧的想法,有时会导致一个人陷入麻烦,虽然它也是一个挑战,往往是有趣的。生成所谓最佳拟合模型的不同方法是本章的重点。它围绕着在描述模型的质量拟合可用数据时使用什么标准的想法,以及如何实现明确选择的标准。
我一直使用”显式”这个词,并且有很好的理由,但是需要一些解释。很多人都有过对数据进行线性回归拟合的经验,但是,根据我的经验,很少有人意识到,当他们拟合这样一个模型时,他们假设使用了加性正态随机残差(正态误差) ,并且他们正在最小化这些残差的平方和。根据上述四个要求,当将一个线性回归应用到一个数据集时,线性关系的假设回答了第二个要求,正态误差的使用(附加常数方差的假设)回答了第三个要求,平方和的最小化是满足第四个要求的选择。通常情况下,最好是明确地了解自己在做什么,而不是仅仅出于习惯或模仿他人。为了对这些模型拟合需求做出最合适的选择(即做出可以辩护的选择) ,分析师还需要了解被建模的自然过程。一个人可以假设和断言几乎任何事情,但只有这样的选择可以得到有效的辩护。作为一个更一般的陈述,如果一个人不能为一组选择辩护,那么他就不应该做出这些选择。
4.1.1 最优化
在 Microsoft Excel 中,当对数据进行模型拟合时,使用内置的Excel解算器找到最佳模型参数。这包括设置电子表格,使最佳拟合标准(平方和、最大似然等,见下文)由一个单元格的内容表示,而模型参数和使用的数据则包含在其他相互关联的单元格中。改变一个模型的参数会改变产生的预测值,这反过来又会改变最佳拟合的标准值。一个 “最佳”参数集可以通过寻找能优化观察值和预测值之间的匹配的参数来找到。这听起来很简单,但实际上是一门艺术,其中要做许多假设和决定。在 Excel 求解器中,人们确定了包含模型参数的单元格,然后求解器的内部代码将修改这些值,同时监测 “最佳拟合标准”单元格,直到找到一个最小(或最大)值(或遇到一个例外)。实际上,这样的电子表格设置构成了在Excel中使用求解器的语法。我们将在 R 中使用求解器或优化函数,它们也有一个必要的语法,但它并不比设置电子表格更复杂,只是更抽象而已。
当对单一数据集(如年龄-长度)用2至6个参数进行非动态过程建模时,模型拟合通常是相对简单的。然而,当处理一个种群的动态过程时,可能会变得更加复杂,涉及到补充、个体生长、自然死亡和多个捕鱼船队的捕捞死亡。可能有许多类型的数据,可能有多于几十个甚至几百个参数。在这种情况下,为了调整预测值与观测值的拟合质量,必须使用某种形式的自动优化或非线性求解器。
优化是一个非常大的研究课题,在CRAN任务视图中详细讨论了许多可用的选项。在 CRAN 任务视图:优化和数学编程中可以找到详细的讨论,网址是https://cran.r-project.org/。在本章的学习中,我们将主要使用内置的函数 nlm()(尝试 ?nlm),但也有许多替代方法(包括 nlminb()、optim()等)。如果你要参与模型拟合,那么真的值得阅读 R-CRAN 上关于优化的任务视图,并且作为第一步,探索 nlm() 和 optim() 函数的帮助和例子。
有时有可能猜测出一组参数,产生看似合理的可视拟合,至少对简单的静态模型来说是如此。然而,虽然这种通过目测拟合(fitting-by-eye)可以为估计模型的参数提供可用的起点,但它并不构成将模型与数据拟合的可辩护的标准。这是因为我的 “目测拟合”(或称 “黑暗中的狂刺”)很可能与你的 “目测拟合”(或称 “有根据的猜测”)不同。与其使用这样的观点,不如使用一些更正式定义的模型与数据拟合质量的标准。
这里的重点是如何设置 R 代码,以便使用最小二乘法或最大似然法进行模型参数估计,特别是后者。我们以后对贝叶斯方法的考虑将主要集中在对不确定性的描述上。我们将通过重复的例子和相关的解释来说明模型的拟合过程。目的是阅读本节应该使读者能够建立自己的模型来解决参数值。我们将尝试以一种一般的方式来做这件事,它应该适合于许多问题的调整。
4.2 最佳拟合标准
确定什么是数据的最佳模型拟合通常有三种方法。
一般来讲,模型拟合包括观测变量 \(x\) 与为描述建模过程而提出候选模型所预测值 \(\hat x\) 之间残差平方的最小化(ssq()):
\[ ssq = \sum_{i=1}^n (x_i- \hat x_i)^2 \qquad(4.1)\]
其中 \(x_i\) 是 \(n\) 个观测中的第 \(i\) 个观测值,\(\hat x_i\) 是给定观测值 \(i\) 的模型预测值(例如,如果 \(x_i\) 为鱼 \(i\) 的年龄-体长,则 \(\hat x_i\) 为一些候选生长模型中得到的鱼 \(i\) 的年龄-体长预测值)。\(\hat x\) 中的 \(\hat{}\) 表示 \(x\) 的预测值。
或者,模型拟合可以涉及最小化负对数似然(在本书中为-veLL 或 negLL),这需要确定1)定义的模型结构,2)一组模型参数和 3)残差的期望概率分布的情况下,每个观测数据点的似然有多大。最小化负对数似然相当于最大化所有似然的乘积或所有数据点的对数似然总和。给定一个观测值 \(x\) 的集合,一个可以预测 \(\hat x\) 的模型结构,以及一组模型参数 \(\theta\) ,那么这些观测值的总似然定义为:
\[ \begin{aligned} {L} &= \prod\limits_{i=1}^{n}{{L}\left( {x_i|\theta}\right )} \\ {-veLL} &= -\sum\limits_{i=1}^{n}{ \log{({L}\left( {x_i|\theta}\right )})} \end{aligned} \qquad(4.2)\]
其中 \(L\) 为总似然,等于\(\prod L(x|\theta)\) 或给定参数值 \(\theta\) 每个观测值 \(x\) 的概率密度(似然)积(在每种情况下,离期望值 \(\hat x\) 越远,似然越低)。-veLL 是给定候选模型参数 \(\theta\) 时观测值 \(x\) 的总负对数似然,每个观测点 \(x\) 的 \(n\) 对数似然的负数和。 我们使用对数似然,因为大多数似然是非常小的数值,当与许多其他非常小的数字相乘时,会变得非常小,以至于有可能导致浮点溢出的计算机错误。对数变换将乘法变为加法,避免了这种风险( \(\prod\) 转变为 \(\Sigma\) )。
第三种方法是使用贝叶斯方法,该方法使用先验概率,即在模型拟合中给予每个备选参数向量的初始相对权重。贝叶斯方法结合并更新任何关于最可能的模型参数的先验知识(先验概率),以及在不同的候选参数向量 \(\theta\) 下任何新数据的似然。就我们的目的而言,贝叶斯方法和最大似然法之间的两个关键区别是包含先验似然和重新缩放数值,以便使后验概率的总和达到1.0。重要的一点是,将给定一组参数的数据似然转换为给定数据参数的真实概率。给定数据 \(x\) 的特定参数集 \(\theta\) 的后验概率定义为:
\[ P(\theta|x)=\frac{L(x|\theta)P(\theta)}{\sum\limits_{i=1}^{n}{\left[ L(x_i|\theta)P(\theta)\right]}} \qquad(4.3)\]
其中 \(P(\theta)\) 为参数集 \(\theta\) 的先验概率,通过给定参数 \(\theta\) 的数据 \(x\) 似然、\(L(x|\theta)p(\theta)\) 进行更新,除数 \(\sum_{i=1}^n[L(x_i|\theta)P(\theta)]\) 对结果重新缩放或归一化,因此在给定数据的情况下,所有参数向量 \(\sum P(\theta|x)\) 的后验概率之和为 1.0。最终 公式 4.3 是一个近似值,因为除数中的总和实际上应该是一个连续分布的积分,但在实践中,近似值就足够了,而且是处理复杂渔业模型参数时的唯一实际选择,其后验分布没有简单的分析解。
这里我们将主要关注负对数似然的最小化(相当于最大似然)。尽管其他方法也会得到一些关注。当我们探讨不确定性的特征时,贝叶斯方法将得到更多的关注。
微软的Excel在很多方面都是很好的软件,但是实现最大似然法,特别是贝叶斯法往往是缓慢和笨拙的,它们更适合于在R中实现。
识别平方残差之和、最大似然法和贝叶斯法并不是一个详尽的清单,它是在对数据进行模型拟合时可能使用的标准。例如,可以使用 “绝对残差之和”(sum of absolute residuals, SAR),它通过使用残差的绝对值而不是将其平方化来避免合并正负残差的问题 (Birkes 和 Dodge 1993)。尽管存在这种最佳模型拟合的替代标准,我们将只关注上述三种。其他更常用的替代方法包括所谓的稳健方法,这些方法致力于减少现有数据中的离群值,或极端的、被认为是不典型的值的影响。如前所述,优化是一个庞大而详细的研究领域,我向你推荐它的研究,并祝你好运。
4.3 R语言中的模型拟合
虽然覆盖参数空间的网格搜索可能是寻找最佳参数集的一种可能的方法,但随着参数数量增加到两个以上,它将变得越来越难操作,直到最后变得不可行。我们将不再考虑这种可能性。相反,为了便于寻找最佳参数集,我们需要一个用软件实现的非线性优化器。
R系统有一系列不同的优化函数,每个函数都使用不同的算法(请参见CRAN任务中关于优化的内容)。解算函数(nlm())和其他函数一样,需要给出一个参数值的初始猜测,然后这些初始参数值由优化函数改变,在每次改变时,预测值会像ssq() 或negLL() 一样重新计算。优化函数,如nlm(),继续改变参数值(它们如何做到这一点是算法不同的地方),直到找到一个组合,根据所选择的任何标准被定义为 “最适合”(或无法找到进一步的改进)。渔业种群评估模型通常有许多参数,数量在10或100个左右(一些有更多的参数,需要更多的专业软件,例如 Daid A. Fournier, Hampton, 和 Sibert (1998); David A. Fournier 等 (2012); Kristensen 等 (2016) )。在本书中,我们不会估计大量的参数,但无论数量多少,其原理都是相似的。
4.3.1 模型需求
讨论模型拟合的理论是有帮助的,但并没有阐明如何在 R 中实现在实践中拟合模型。优化软件用于改变参数向量内的值,但我们需要为其提供重复计算预测值的方法,该预测值将用于与观测值进行多次比较以找到最佳解决方案(如果成功的)。我们需要开发可以重复调用的代码块,这正是设计 R 语言函数的目的。为了在 R语言 中实现对现实世界问题的模型拟合,我们需要考虑四个形式要求:
来自所研究系统的观测(数据)。这可能是渔业中一个具有观测到的渔获量、cpue、渔获量的年龄和长度组成等,或者它可能是更简单的东西,例如鱼样本的观测到的长度和相关的年龄(但是如何将其放入 R ?),
第一个 R语言函数,表示系统的候选模型,当提供参数向量时,该函数用于计算预测值,以便与任何可用的观测值进行比较,
第二个 R语言 函数,计算选定的最佳拟合标准、最小化最小二乘或最小化负对数似然,以便将观测值与预测值进行比较。这需要能够返回单个值,反映输入参数和数据,然后可以通过最终所需的函数最小化,即
第三个R 语言函数(我们将倾向于使用
nlm())来自动优化所选最佳拟合标准的值。
因此,需要输入数据和三个函数( 图 4.1 )但是,因为我们可以使用内置函数来进行优化,模型拟合通常需要编写最多两个函数,一个用于从使用的任何模型计算预测值另一个用于计算拟合标准(有时,在更简单的练习中,这两个可以组合成一个函数)。
我们在本书中假设读者至少熟悉模型拟合背后的概念,如拟合线性回归,因此我们将直接转向非线性模型拟合。这些相对简单的示例的主要目的是介绍 R 中可用求解器的使用和语法。
4.3.2 年龄-体长示例
将模型拟合到数据仅仅意味着估计模型的参数,以便其预测与观测结果相匹配,以及根据选择的最佳拟合标准。作为在 R 中将模型拟合到数据的第一个说明,我们将使用一个简单的示例用著名的 von Bertalanffy 生长曲线 (von Bertalanffy, 1938) 拟合一组年龄-长度数据。这样的数据集包含在 R 包 MQMF(尝试 ?LatA)中。要使用您自己的数据,一种选择是生成一个逗号分隔的变量 (csv) 文件,其中包含最少的年龄和长度列,每个列都有一个列名(LatA 仅有年龄和长度列;请参阅其帮助页面)。可以使用 laa <- read.csv(file="filename.csv", header=TRUE) 将此 csv 文件读入 R中。
von Bertalanffy 长度-年龄生长曲线表示为:
\[ \begin{aligned} & {{\hat{L}}_t}={L_{\infty}}\left( 1-{e^{\left( -K\left( t-{t_0} \right) \right)}} \right) \\ & {L_t}={L_{\infty}}\left( 1-{e^{\left( -K\left( t-{t_0} \right) \right)}} \right)+\varepsilon \\ & {L_t}= {\hat{L}}_t + \varepsilon \end{aligned} \qquad(4.4)\]
其中 \(\hat L_t\) 为年龄 \(t\) 的期望或预测长度,\(L_{\infty}\) 为渐近平均最大长度,\(K\) 为是决定达到最大值的增长率系数,\(t_0\) 为物种长度0时的假设年龄(von Bertalanffy, 1938),一旦我们有了\(L_{\infty}\),\(K\) ,\(t_0\) 的估算值(或假设值),该非线性方程就提供了一种预测不同年龄的年龄-长度的方法。在拟合数据模型时,使用 公式 4.4 中的下面两个方程,其中\(L_t\) 为观测值,等于预测值加上正态随机离差\(\varepsilon = N(0, \sigma^2)\) ,其中的每个值可能是正的或负的(某一年龄的观测值可能大于或小于期望长度)。最下面的方程实际上是关于决定使用什么剩余误差结构。在本章中,我们将描述生态学和渔业中使用的一系列可供选择的误差结构。它们并非都是可加的,有些是用函数关系而不是常数定义的(如\(\sigma\))。
关于 公式 4.4 是非线性的表述是明确的,因为早期估计 von Bertalanffy ( vB() )生长曲线参数值的方法涉及各种旨在近似线性化曲线的变换(例如 Beverton和Holt, 1957)。在20世纪50年代末和60年代,拟合 von Bertalanffy 曲线不是一件小事。令人高兴的是,不再需要这样的转换,这样的曲线拟合也变得很简单。
4.3.3 其它的生长模型
个体生长的研究文献很多,描述生物体生长的模型多种多样(Schnute and Richards, 1990)。自Beverton和Holt (1957)引入以来,von Bertalanffy (vB() )曲线一直是主要的渔业模型,已被渔业科学家广泛应用。然而,只是因为该模型非常普遍命令使用,对于所有物种来说,并不一定意味着该模型总是提供生长的最佳描述。模型选择是渔业建模中一个至关重要但经常被忽视的方面 (Burnham 和 Anderson 2004; Helidoniotis 和 Haddon 2013)。这里两种替代 vB()的两种模型可能是 Gompertz 生长曲线 (Gompertz, 1925):
\[ \hat{L_t} =ae^{-be^{ct}} \text{ or } \hat{L_t}=a \exp(-b \exp(ct)) \qquad(4.5)\]
以及广义Michaelis-Menten 方程(Maynard Smith and Slatkin, 1973; Legendre and Legendre, 1998):
\[ {{\hat{L}}_{t}}=\frac{at}{b+{{t}^{c}}} \qquad(4.6)\]
每个模型也有 a、b 和 c 三个参数,每个模型都能对生长过程的经验数据作出令人信服的描述。可以对某些参数进行生物学解释(如最大平均长度),但这些模型最终只提供了对生长过程的经验描述。如果把模型解释为反映了现实,就会导致完全不可信的预测,如不存在一米长的鱼(Knight,1968 )。在文献中,参数可以有不同的符号(例如,Maynard Smith 和 Slatkin(1973)用 \(R_0\) 代替 \(a\) 表示 Michaelis-Menton),但基本结构形式是相同的。在对 MQMF 的年龄-长度数据集 \(LatA\) 中的鱼类进行 von Bertalanffy 生长曲线拟合后,我们可以利用不同模型来说明尝试这些替代模型的价值,并对应该使用哪种模型保持开放的心态。这个问题在我们讨论不确定性时会再次出现,因为我们可以从不同的模型中得到不同的结果。在对任何自然过程建模时,模型选择都是需要做出的重大决定之一。重要的是,通过这种方式尝试不同的模型,还能强化模型与数据拟合的过程。
4.4 残差平方和
数据拟合模型的经典方法称为 “最小残差平方和”(见 公式 4.1 和 公式 4.7 ),或更常称为 “最小二乘法”。这种方法被认为是高斯提出的(Nievergelt, 2000, 引用了高斯 1823 年用拉丁文撰写的一本书的译文:Theoria combinationis observationum erroribus minimis obnoxiae)。无论如何,最小二乘法符合两个多世纪以来用于确定一组预测值与观测值最佳拟合的策略。这种策略就是确定一个所谓的目标函数(最佳拟合标准),根据函数结构,可以将其最小化或最大化。就残差平方和而言,我们需要从相关的观测值中减去每个预测值,将不同的结果平方(以避免出现负值),然后将所有值相加,并使用数学(解析解)或其他方法将该相加值最小化:
\[ ssq=\sum\limits_{i=1}^{n}{{{\left( {{O}_{i}}-{\hat{E}_{i}} \right)}^{2}}} \qquad(4.7)\]
其中,\(sqq\) 为 n 个观测值的残差平方和,\(O_i\) 为第\(i\) 个观测值,\(E_i\)为第第\(i\) 个观测值的期望值或预测值。MQMF 包中的ssq 函数仅仅是一个封装器,它调用了用于生成预测值的任何函数,然后计算并返回平方差和。根据不同问题的复杂程度和数据输入,我们通常需要创建新的函数作为封装。ssq() 很好地说明了这样一个事实,即在一个传递给函数的参数中,也可以传递其他函数(在本例中,在 ssq()内我们调用了传递给 funk 的函数,当然在使用ssq()时,我们输入的是与当前问题相关的实际函数,也许是vB,注意在用作函数参数时没有括号)。
4.4.1 最小二乘法的假设
最小二乘方法的一个主要假设是,残差项呈正态分布,所有观测变量值具有相等的方差;即在\(\varepsilon = N(0, \sigma^2)\) 中,\(\sigma^2\) 是常数。如果以任何方式对数据进行变换,则变换对残差的影响可能违反这一假设。相反,如果残差以系统的方式变化,则转换可以标准化残差方差。因此,如果数据是对数正态分布,那么对数变换将使数据标准化,然后可以有效地使用最小二乘。与往常一样,考虑或可视化数据和残差的形式(由拟合模型产生)是一种很好的做法。
4.4.2 数值求解
渔业科学中大多数有趣的问题都没有解析解(如线性回归),有必要使用数值方法通过定义的”最佳拟合”标准(如最小残差平方和(最小二乘))来寻找最佳拟合模型。这显然会涉及到一点R编程,但是R的一个很大的优势是,一旦你开发了一套分析方法,就可以直接地将其应用到新的数据集。
在下面的示例中,我们用 MQMF 中的一些实用函数来辅助描述。我们需要 5 个函数拟合和比较上文定义的3种不同的生长模型,其中4个需要编写。前3个函数用于估计与观测数据进行比较的各年龄长度预测值。本例有3个候选模型函数分别对应3种不同的生长曲线:vB()、 Gz()和 mm()。第4个函数用作计算预测值及其相关观测值的平方和残差。这里将使用 MQMF 中的函数 ssq()(你应该检查并理解其代码)。该函数返回单一数值,该值将由最后一个函数 nlm()最小化,该函数需要自动最小化求解。R 函数 nlm()使用用户定义的广义函数,用 \(f\) 表示 (尝试 args(nlm),或formals(nlm)以查看完整的参数列表),用于计算最小值(在本例中为 ssq()),而ssq()又使用预测生长曲线中各年龄长度的函数(例如vB())。如果我们使用不同的生长曲线函数(例如Gz()),只需将nlm()调用代码中指向vB() 的地方改为 Gz() ,并修改参数值以适应 Gz()函数,以便代码产生可用的结果。从根本上说,nlm()通过改变输入参数(称作 p )来最小化ssq(),无论选择哪个参数,都会改变生长函数vB()、Gz()或mm()的结果,。
nlm()只是 R 中用于非线性优化的函数之一,候选函数包括 optim()和 nlminb()(请阅读 nlm中的文档,CRAN 上关于优化的任务视图列出了旨在解决优化问题的包)。
代码
library(MQMF)
library(ggplot2)
#setup optimization using growth and ssq
data(LatA) # try ?LatA assumes library(MQMF) already run
#convert equations 4.4 to 4.6 into vectorized R functions
#These will over-write the same functions in the MQMF package
vB <- function(p, ages) return(p[1]*(1-exp(-p[2]*(ages-p[3]))))
Gz <- function(p, ages) return(p[1]*exp(-p[2]*exp(p[3]*ages)))
mm <- function(p, ages) return((p[1]*ages)/(p[2] + ages^p[3]))
#specific function to calc ssq. The ssq within MQMF is more
ssq <- function(p,funk,agedata,observed) { #general and is
predval <- funk(p,agedata) #not limited to p and agedata
return(sum((observed - predval)^2,na.rm=TRUE))
} #end of ssq
# guess starting values for Linf, K, and t0, names not needed
pars <- c("Linf"=27.0,"K"=0.15,"t0"=-2.0) #ssq should=1478.449
ssq(p=pars, funk=vB, agedata=LatA$age, observed=LatA$length) [1] 1478.449ssq()函数取代了全局环境中的 MQMF::ssq()函数,但也返回一个数值,例如上面的 1478.449,它是 nlm()函数的第一个输入,也是需要最小化的值。
4.4.3 将函数作为参数传递给其它函数
在上例中,我们定义了一些用于模型拟合数据所需的函数,确定了要比较的生长模型,也定义了计算平方和的函数。刚刚做的一个非常重要的方面是,为了计算平方和,我们将 vB()函数作为参数传递给 ssq()函数。这意味着我们传递了一个函数,它有参数,作为另一个函数的参数之一。你可以在这里看到潜在的混乱,所以有必要集中精力,保持清晰。目前,我们定义 ssq()的方式似乎并没有那么引人注目,因为我们已经在对ssq()的调用中显式地定义了两个函数的参数。但是 R 有一些妙招,我们可以用它来泛化包含其他函数作为参数的函数,主要的一个使用了神奇的省略号…,对于任何R函数,除非实参在其定义中设置了默认值,否则每个实参都必须给定一个值。在上面的ssq()函数中,我们包含了仅由 ssq() 使用的参数( funk 和 observed ),以及仅由函数 funk使用的参数( p 和 agedata)。这在本例子中很有效,因为我们故意将生长函数定义为具有相同的输入参数,但如果我们想使用的 funk 有不同的输入,可能是因为我们拟合的是选择性曲线而不是生长曲线,该怎么办?显然,我们需要编写一个不同的 ssq() 函数。为了允许在更多情况下重用更通用的函数,R 的作者(R Core Team, 2019)包含了这个概念 …,它将匹配其他方式不匹配的任何参数,因此可用于输入funk 函数的参数。因此,我们可以这样重新定义 ssq():
代码
# Illustrates use of names within function arguments
vB <- function(p,ages) return(p[1]*(1-exp(-p[2] *(ages-p[3]))))
ssq <- function(funk,observed,...) { # only define ssq arguments
predval <- funk(...) # funks arguments are implicit
return(sum((observed - predval)^2,na.rm=TRUE))
} # end of ssq
pars <- c("Linf"=27.0,"K"=0.15,"t0"=-2.0) # ssq should = 1478.449
ssq(p=pars, funk=vB, ages=LatA$age, observed=LatA$length) #if no [1] 1478.449代码
ssq(vB,LatA$length,pars,LatA$age) # name order is now vital! [1] 1478.449这意味着 ssq() 函数现在更加通用,可以与任何输入函数一起使用,这些输入函数可用于生成一组预测值,以便与一组观测值进行比较。MQMF 中的 ssq() 函数就是这样实现的;查阅帮助 ?ssq。一般的想法是,您必须定义主函数中使用的所有参数,但任何仅在被调用函数(此处称为 funk )中使用的参数都可以在 …中传递。最好是显式地命名参数,这样它们的顺序就无关紧要了,并且您需要非常小心地键入,如果您拼错了通过…传递的参数的名称,并不一定会出错!例如,使用大写的 LatA$Age 而不是 LatA$age 不会出错,但会导致结果为 0 而不是 1478.440。这是因为 LatA$Age = NULL,即使输入不正确也是有效的。很明显,… 可能非常有用,但如果你像我一样输入错误,其本身也是有风险的。
代码
# Illustrate a problem with calling a function in a function
# LatA$age is typed as LatA$Age but no error, and result = 0
ssq(funk=vB, observed=LatA$length, p=pars, ages=LatA$Age) # !!! [1] 0如果你匆忙行事,没有给参数命名,那么如果你弄错了参数顺序,也会失败。例如,如果你要输入的是ssq(LatA$length, vB, pars, LatA$age)而不是ssq(vB, LatA$length, pars, LatA$age),就会出现错误:Error in funk(…): could not find function ” funk “。为了以防万一,你可以自己试试。对你的代码进行试验几乎没什么坏处,不会弄坏你的电脑,而你可能会学到一些东西。
4.4.4 模型拟合
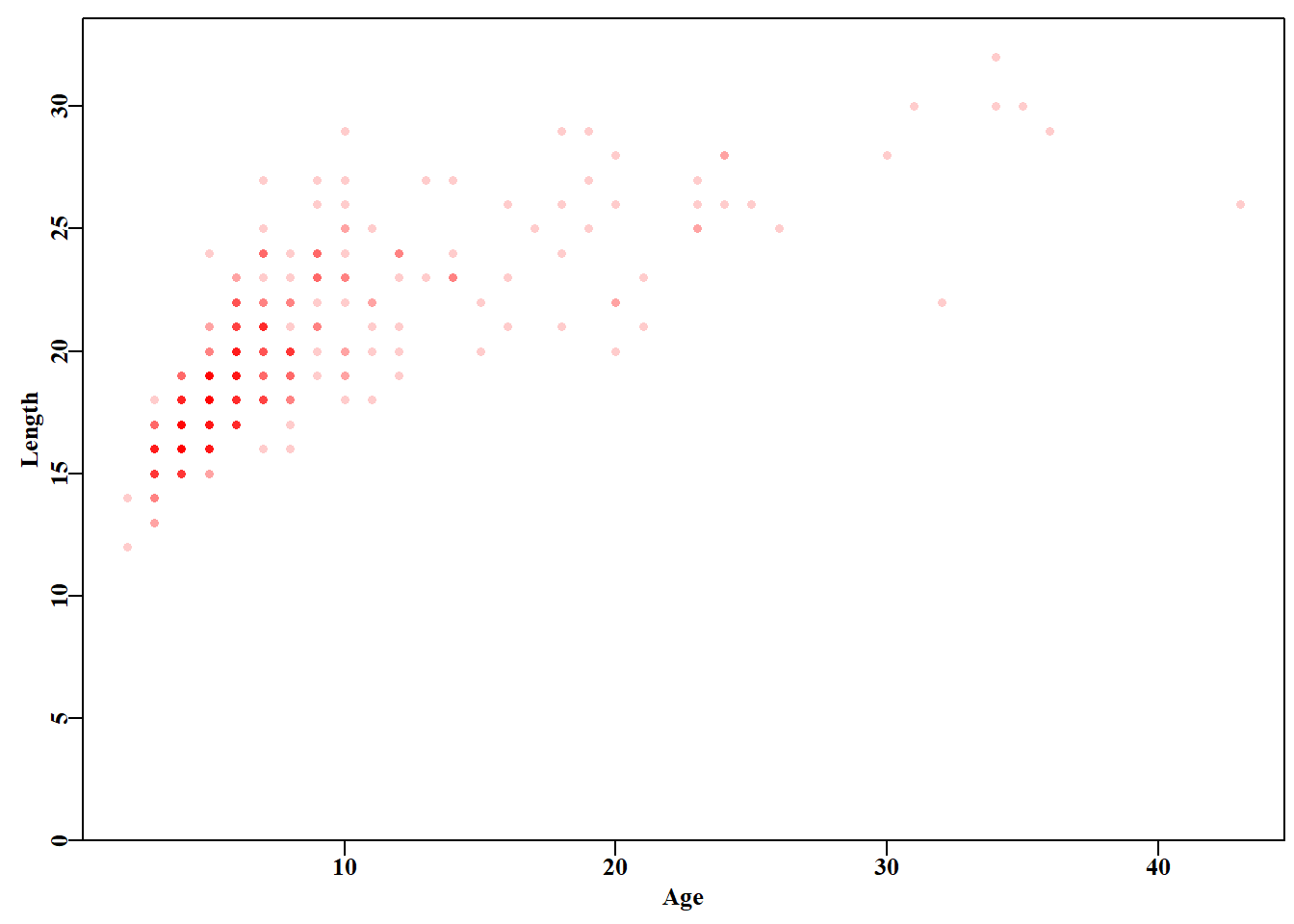
如果我们绘制 LatA 数据集图( 图 4.2 ),可以看到一些典型的年龄-长度数据。图中有 358 个点(试试 dim(LatA)),许多点彼此重叠,但是当我们使用 plot()函数中 rgb()选项来改变图中颜色的透明度时,较高年龄组鱼类的颜色相对稀疏性就会显现出来。另外,我们可以使用 jitter()为每个绘制点的位置添加噪声,以查看数据点的相对密度。每当你处理经验数据时,总是值得你花时间至少将其绘制成画并探索其属性。
代码
#plot the LatA data set Figure 4.2
parset() # parset and getmax are two MQMF functions
ymax <- getmax(LatA$length) # simplifies use of base graphics. For
# full colour, with the rgb as set-up below, there must be >= 5 obs
plot(LatA$age,LatA$length,type="p",pch=16,cex=1.2,xlab="Age Years",
ylab="Length cm",col=rgb(1,0,0,1/5),ylim=c(0,ymax),yaxs="i",
xlim=c(0,44),panel.first=grid())
# ggplot(data = LatA, aes(x = age, y = length)) +
# geom_point(size = 3, color = "red", alpha = 0.2) +
# labs(x = "Age Years",
# y = "Length cm") +
# theme_bw() 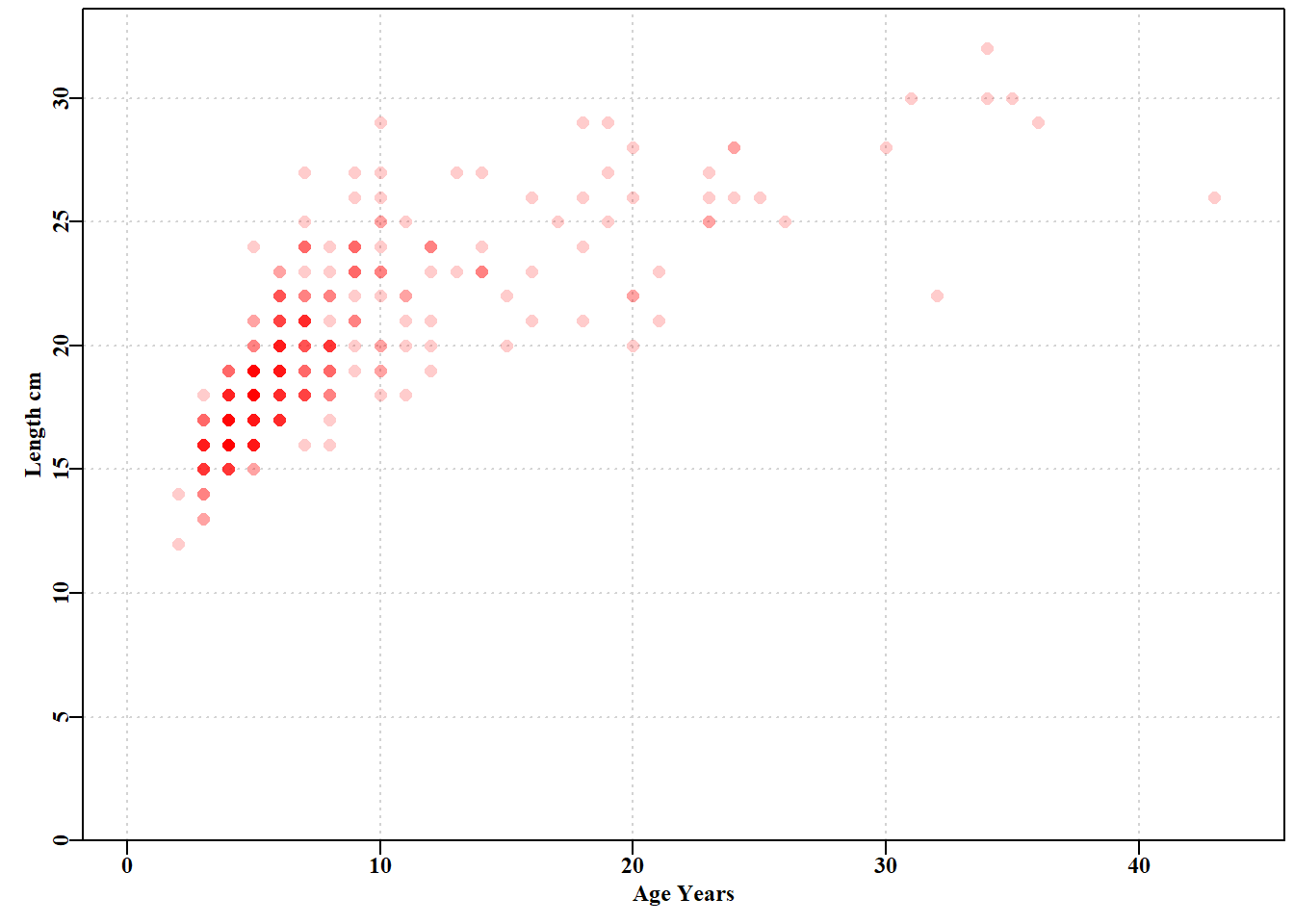
与其继续推测参数值并手动修改它们,我们可以使用 nlm() 或 optim()或 nlminb(),它们的语法不同)来拟合所选的 LatA 数据的生长模型或曲线。这不仅说明了nlm()的语法,还说明了另外两个 MQMF 实用R函数 magnitude()和 outfit()的使用(请查阅?nlm、?magnitude和 ?outfit)。还可以查看每个函数中的代码(在控制台中输入每个函数的名称,不带参数或括号)。从现在起,我将减少提示你查看所使用函数细节的次数,但是如果看到一个新的函数,希望现查看其帮助、语法,尤其是代码是有意义的,就像查看每个所用变量的内容一样。
3 个生长模型中的每一个都需要估计 3 个参数,我们需要对每个参数进行初始猜测,以启动 nlm()求解。我们所做的就是为 nlm()函数的每个形参/实参提供值。此外,我们还使用了 2 个额外的参数,typsize 和 iterlim。typesize 在 nlm()帮助中定义为”每个参数最小值的估计”。加入这 2 个参数一般有助于稳定搜索算法,因为它可以确保对每个参数值迭代变化尺度大致相同。一种非常常见的替代方法(我们将在更复杂的模型中使用)是在输入 nlm()时对每个参数进行对数变换,然后在调用的函数中对它们进行反变换,以计算预测值。但是,这只能在保证参数始终为正值情况下才可行。例如,对于 von Bertalanffy 曲线,\(t_0\) 参数通常是负值,因此应使用 magnitude()而不是对数变换方法。默认的 iterlim=100意味着最多迭代 100 次,这有时是不够的,所以如果迭代达到 100 次,您应该将该数值增加到 1000 。你很快就会发现,在每次模型拟合过程中,唯一改变的是ssq()中的 funk 所指向的函数和初始参数值。这可以通过有意识地构建生长函数,使其使用完全相同的参数(通过…传递)。您也可以尝试在不设置 typsize 和 interlim 选项的情况下运行其中的一个或两个函数。还请注意,我们运行 Michaelis-Menton 曲线时使用了两个略有不同的初始点。
代码
# use nlm to fit 3 growth curves to LatA, only p and funk change
ages <- 1:max(LatA$age) # used in comparisons
pars <- c(27.0,0.15,-2.0) # von Bertalanffy
bestvB <- nlm(f=ssq,funk=vB,observed=LatA$length,p=pars,
ages=LatA$age,typsize=magnitude(pars))
outfit(bestvB,backtran=FALSE,title="vB"); cat("\n") nlm solution: vB
minimum : 1361.421
iterations : 24
code : 2 >1 iterates in tolerance, probably solution
par gradient
1 26.8353971 -1.134306e-04
2 0.1301587 -6.198614e-03
3 -3.5866989 8.330772e-05代码
nlm solution: Gz
minimum : 1374.36
iterations : 28
code : 1 gradient close to 0, probably solution
par gradient
1 26.4444554 2.725617e-05
2 0.8682518 -6.452607e-04
3 -0.1635476 -2.042292e-03代码
nlm solution: MM
minimum : 1335.961
iterations : 12
code : 2 >1 iterates in tolerance, probably solution
par gradient
1 20.6633224 -0.02622725
2 1.4035207 -0.37744267
3 0.9018319 -0.05039237代码
nlm solution: MM2
minimum : 1335.957
iterations : 25
code : 1 gradient close to 0, probably solution
par gradient
1 20.7464274 8.464689e-06
2 1.4183164 -3.856394e-05
3 0.9029899 -1.297065e-04这些都是数值解,它们不能保证是正确的解。请注意,第一个 Michaelis-Menton 解(从 26.2,1,1 开始)的梯度相对较大,但它的 SSQ(1335.96) 非常接近第二个 Michaelis-Menton 模型拟合,而且比 vB 或 Gz 曲线更小(更好)。然而,梯度值表明该模型的拟合可以而且应该得到改进。如果您将参数 a(首个 MM 参数)的初始参数估计值从上次模型拟合中的 26.2 降到了 23,我们就会得到稍有不同的参数值、稍小的 SSQ 以及更小的梯度,从而更有把握地认为结果是个真正的最小值。实际上,如果要运行cbind(mm(bestMM1$estimate,ages), mm(bestMM2$estimate,ages)),可以计算出预测值的差异从 -0.018 到 0.21%,而如果将 vB 预测值包括在内,MM2 与 vB 预测的差异从 -6.15 到 9.88% (忽略 40.6% 的最大偏差)。你也可以尝试从 vB 模型的估计中省略typsize 参数,这样仍然会得到最佳结果,但可查看梯度以了解为什么使用 typsize 有助于优化。在设置这些示例时,偶尔运行 Gz()模型会出现 steptol 可能太小的注释,将其从默认的 1e-06 改为 1e-05 可以很快解决这个问题。如果您遇到了这种情况,请在nlm()命令中添加一条语句 steptol=1e-05,看看诊断是否有所改善。
显而易见的结论是,我们应该经常查阅 nlm()的诊断注释,考虑得到的解的方案的梯度,并且使用多组初始参数猜测,以确保得到稳定的解。数值求解以软件实现为基础,用于决定何时停止迭代的规则有时会被次优解所欺骗。我们的目标是找到全局最小值,而不是局部最小值。任何非线性模型都可能产生此类次优解,因此自动拟合此类模型并非易事。在这种情况下,永远不要假设在这种情况下你得到的第一个答案一定是你正在寻找的最佳答案,即使描绘的模型拟合看起来是可以接受的。
在函数调用中,如果你为每个参数命名,那么严格来讲,顺序并不重要,但我发现一致的用法可以简化代码的阅读,因此即使使用显式名称,也建议使用标准顺序。如果我们不使用显式名称,则 nlm()的语法要求首先定义函数最小化(f)。此外,它还要求 f 函数,无论它是什么,在 p 参数中使用初始参数猜测,如果未命名,则必须排在第二位。如果你在控制台中输入 formals(nlm)或 args(nlm),就可得到可以输入到函数的可能参数以及它们的默认值(如果存在):
代码
#The use of args() and formals()
args(nlm) # formals(nlm) uses more screen space. Try yourself. function (f, p, ..., hessian = FALSE, typsize = rep(1, length(p)),
fscale = 1, print.level = 0, ndigit = 12, gradtol = 1e-06,
stepmax = max(1000 * sqrt(sum((p/typsize)^2)), 1000), steptol = 1e-06,
iterlim = 100, check.analyticals = TRUE)
NULL正如所见,首先要最小化函数 f (在本例中是 ssq() ),然后是初始参数 p,它必须是f所指向的任何函数所需的第一个参数。接着是省略号(三个点),它概括了任何函数f的 nlm()代码,其后是可能的参数集,所有这些参数都具有默认值。我们修改了 typsize 和 iterm (有时也修改了Gz() 中的 steptol);请参阅 nlm()帮助以获得对每种方法的解释。
在R中,”…“ 实际上指的是所需的任何其他输入,例如函数f指向的任何参数(本例中为ssq)。如果 Et ?ssq查看参数或代码或帮助,将会看到所需函数 funk,该函数将用于计算相对于ssq()的下一个所需输入的期望值,为观测值的向量(如\(O_i-E_i\))。请注意,这里没有明确提到 funk 使用的参数,这些参数假定是通过 …. 传递的。在对 ssq()的每次调用中,我们都显式地填充了这些参数,例如nlm(f=ssq,funk=Gz, observed=LatA$length, p=pars, ages=LatA$age,)。这样,所有要求都已满足,ssq()就可以开始工作。如果不小心忽略了ages=LatA$age参数,那么在这种情况下,R 会出现如下揭示:Error in funk(par, independent) : argument “ages” is missing, with no default(我相信你会相信我的,但你自己试试也无妨!)。
就生长曲线模型拟合而言,绘制结果提供了一个直观的比较,说明了三条生长曲线之间的差异(Murrell, 2011)。
代码
#Female length-at-age + 3 growth fitted curves Figure 4.3
predvB <- vB(bestvB$estimate,ages) #get optimumpredicted lengths
predGz <- Gz(bestGz$estimate,ages) # using the outputs
predmm <- mm(bestMM2$estimate,ages) #from the nlm analysis above
ymax <- getmax(LatA$length) #try ?getmax or getmax [no brackets]
xmax <- getmax(LatA$age) #there is also a getmin, not used here
parset(font=7) # or use parsyn() to prompt for the par syntax
plot(LatA$age,LatA$length,type="p",pch=16, col=rgb(1,0,0,1/5),
cex=1.2,xlim=c(0,xmax),ylim=c(0,ymax),yaxs="i",xlab="Age",
ylab="Length (cm)",panel.first=grid())
lines(ages,predvB,lwd=2,col=4) # vB col=4=blue
lines(ages,predGz,lwd=2,col=1,lty=2) # Gompertz 1=black
lines(ages,predmm,lwd=2,col=3,lty=3) # MM 3=green
#notice the legend function and its syntax.
legend("bottomright",cex=1.2,c("von Bertalanffy","Gompertz",
"Michaelis-Menton"),col=c(4,1,3),lty=c(1,2,3),lwd=3,bty="n")
# ggplot() +
# geom_point(data = LatA, aes(x = age, y = length),
# color = "red", alpha = 0.2) +
# geom_line(aes(x = ages, y = predvB), color = "blue") +
# geom_line(aes(x = ages, y = predGz), color = "black") +
# geom_line(aes(x = ages, y = predmm), color = "green") +
# theme_bw()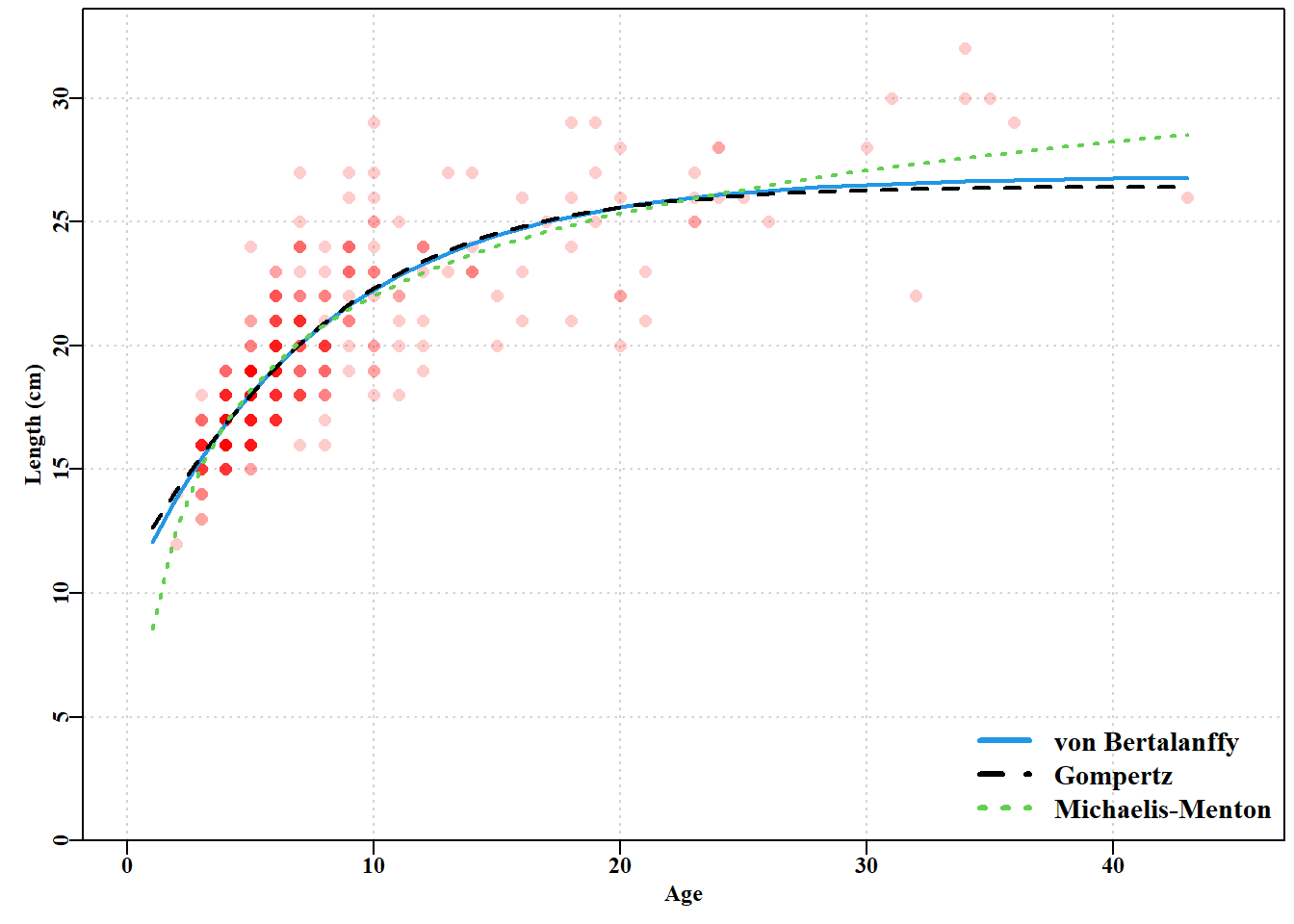
在图中使用的 rgb() 函数意味着颜色强度代表观测数量,最强烈的颜色至少表示有五个观测值。很明显,在这份数据中, vB() 和 Gz() 曲线在大部分观测范围内几乎重合,而 mm() 曲线与其他两条曲线偏离,但主要是在极端值处。Michaelis-Menton 曲线被强制通过原点,而另外两条曲线则不受这种限制(尽管这个想法可能更接近现实)。可以包括幼鱼长度来将高姆珀茨曲线和 von Bertalanffy 曲线向下拉。但生物生长过程很复杂。许多鲨鱼和鳐鱼是胎生,确实在发育后期开始生活时体型显著大于零。始终要记住,这些曲线只是数据的经验性描述,反映现实的能力有限。
大部分可用数据集中在 3 至 12 龄之间(尝试 table(LatA$age) ),然后只有 24 龄以上单次出现。在 3 至 24 龄之间,Gompertz 曲线和 von Bertalanffy 曲线基本上遵循相同轨迹,而 Michaelis-Menton 曲线差异很小(你可以尝试以下代码查看实际差异 cbind(ages, predvB, predGz, predmm) )。超出这个年龄范围,差异更大,尽管缺乏年轻动物表明捕捞样本的渔具选择性可能无法充分代表 3 龄以下的鱼类。在拟合相对质量(残差平方和)方面,最终的 Michaelis-Menton 曲线最小 ssq() ,其次是 von Bertalanffy 曲线,然后是 Gompertz 曲线。但每种模型都为 3 至 24 龄(数据最密集范围)之间的生长提供了合理的平均描述。当老年年龄组的数据如此稀疏时,也存在该样本是否代表这些年龄组种群的问题。质疑数据、所用模型及由此产生的解释,是构建自然过程有用模型的重要方面。
4.4.5 目标模型选择
在上述三种生长模型中,最优模型拟合定义为使预测值与实测值之间的平方和残差最小。根据这一标准,第二个生长模型 Michaelis-Menton 曲线比 von Bertalanffy 曲线和 Gompertz 曲线更适合。但我们真的能说第二条 Michaelis-Menton 曲线比第一条曲线”更好”拟合吗?就最终溶液的梯度而言,第二条曲线显然更好,但严格的拟合标准只是最小 SSQ,差异小于 0.01 个单位。模型选择通常是使用参数的数量和根据所选标准的拟合质量之间的权衡。如果我们设计一个具有更多参数的模型,这通常会导致更大的灵活性和更接近观测数据的改进能力。在极端情况下,如果我们有和观测值一样多的参数,我们可以有一个完美的模型拟合,但是,当然,我们对我们正在建模的系统一无所知。LatA 数据集有 358 个参数,这显然是过度参数化的情况,但如果我们只将参数数量增加到10个呢?毫无疑问,曲线的形状会很奇怪,但 SSQ 可能会更低。Burnham 和 Anderson(2002) 详细讨论了参数数量和模型与数据的拟合质量之间的权衡关系。在 20 世纪 70 年代,人们开始使用信息论来开发一种量化模型参数和模型拟合质量之间权衡的方法。Akaike(1974) 描述了他的Akaike信息标准(AIC),该标准基于最大似然和信息理论原理(稍后会详细介绍),但幸运的是,Burnham 和 Anderson(2002) 在使用最小平方和残差时提供了另一种选择,这是Atkinson(1980)中包含的一种变体:
\[ AIC=N \left(\log\left(\hat\sigma^2 \right) \right)+2p \qquad(4.8)\]
其中\(N\) 为观测数,\(p\) 为”模型内独立调整参数数量”(Akaike,1974,p716),\(\hat{\sigma}^2\) 为方差的最大似然估计,仅表示残差平方和除以\(N\) 而非 \(N-1\) :
\[ \hat\sigma^2 = \frac{\Sigma\varepsilon^2}{N} = \frac{ssq}{N} \qquad(4.9)\]
即使有了AIC,也很难确定,当使用最小二乘时,差异是否可以被认为是统计上显著的差异。有与方差分析相关的方法,但当使用最大似然时,这些问题能够得到更可靠的回答,所以我们将在后面的部分中解决这个问题。
如果想在拟合模型时获得生物学上合理的或可站得住脚的解释,那么模型选择不能仅仅依赖于统计拟合的质量。相反,它应该反映理论预期(例如,种群中的平均生长是否包括随着时间的推移个体大小的平稳增长,等等)。除了数据的统计拟合之外,这些考虑因素似乎没有得到足够的重视,但只有在出现生物学上不可信的模型结果或提出不可信的模型结构时才变得重要。它显然有助于理解正在建模的过程的生物学期望。
4.4.6 残差选择对模型拟合的影响
在生长模型例子中,我们使用了正态随机偏差,但我们可以问,如果我们使用,例如对数正态偏差,我们是否会得到相同的答案?在这种情况下,我们所需要做的就是在计算残差平方和之前对观测值和预测值进行对数变换(参见下面关于对数正态残差的内容)。
\[ ssq=\sum\limits_{i=1}^{n}{{{\left( \log({O_i})- \log({\hat{E_i}}) \right)}^{2}}} \qquad(4.10)\]
这里我们继续在 outfit()中使用 backtran=FALSE 选项,因为我们是对数据进行对数转换,而不是对参数进行对数转换,因此不需要进行反向转换。
代码
nlm solution: Normal errors
minimum : 1361.421
iterations : 22
code : 1 gradient close to 0, probably solution
par gradient
1 26.8353990 -3.645466e-07
2 0.1301587 -1.578320e-05
3 -3.5867005 3.198205e-07代码
# modify ssq to account for log-normal errors in ssqL
ssqL <- function(funk,observed,...) {
predval <- funk(...)
return(sum((log(observed) - log(predval))^2,na.rm=TRUE))
} # end of ssqL
bestvBLN <- nlm(f=ssqL,funk=vB,observed=LatA$length,p=pars,
ages=LatA$age,typsize=magnitude(pars),iterlim=1000)
outfit(bestvBLN,backtran=FALSE,title="Log-Normal errors") nlm solution: Log-Normal errors
minimum : 3.153052
iterations : 25
code : 1 gradient close to 0, probably solution
par gradient
1 26.4409587 8.898258e-08
2 0.1375784 7.546830e-06
3 -3.2946086 -1.122823e-07在这种情况下,使用正态和对数正态残差产生的曲线几乎没有区别( 图 4.4 )。尽管它们的参数不同(使用 ylim=c(10,ymax) 使差异更明显)。除了视觉上的不同,不同的模型甚至没有可比性。如果我们比较它们各自的平方和残差,一个是 1361.0,另一个只有 3.153。当我们考虑到平方和计算中对数变换的影响时,这并不奇怪。但这意味着我们不能只看表格输出,然后决定哪个版本比另一个更适合数据。它们是严格不相称的,尽管它们使用的是完全相同的模型。不同残差结构的使用需要在考虑相对模型拟合以外的方式进行辩护。这个例子强调,虽然模型的选择显然很重要,但残差结构的选择也是模型结构的一部分,同样重要。
代码
# Now plot the resultibng two curves and the data Fig 4.4
predvBN <- vB(bestvBN$estimate,ages)
predvBLN <- vB(bestvBLN$estimate,ages)
ymax <- getmax(LatA$length)
xmax <- getmax(LatA$age)
parset()
plot(LatA$age,LatA$length,type="p",pch=16, col=rgb(1,0,0,1/5),
cex=1.2,xlim=c(0,xmax),ylim=c(0,ymax),yaxs="i",xlab="Age",
ylab="Length (cm)",panel.first=grid())
lines(ages,predvBN,lwd=2,col=4,lty=2) # add Normal dashed
lines(ages,predvBLN,lwd=2,col=1) # add Log-Normal solid
legend("bottomright",c("Normal Errors","Log-Normal Errors"),
col=c(4,1),lty=c(2,1),lwd=3,bty="n",cex=1.2) 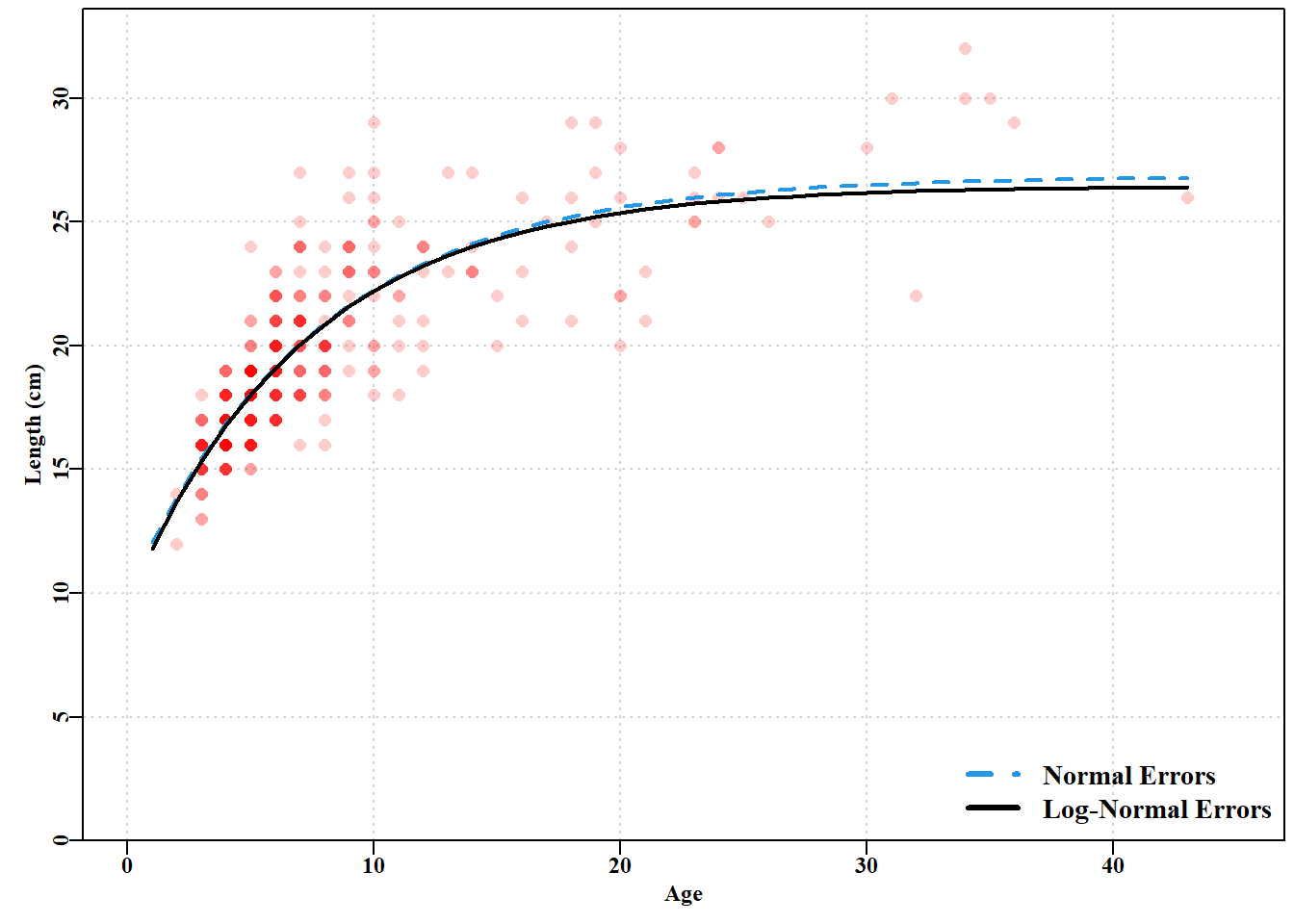
4.4.7 关于初始模型拟合的说明
上面例子中的曲线比较本身就很有趣,不过,我们还说明了 nlm() 的语法以及如何将模型拟合到数据中。将函数作为参数传递给另一个函数的能力(就像这里我们将 ssq 作为 f 传递给 nlm(),将 vB、Gz 和 mm 作为 funk 传递给 ssq())是 R 的优势之一,但也是其复杂性所在。它简化了ssq()等函数的重用,在这些函数中,我们只需改变输入函数,就能从本质上相同的代码中得到完全不同的答案。熟悉这些方法的最佳途径是使用自己的数据集。绘制您的数据和任何模型拟合图,因为如果模型拟合图看起来不寻常,那么很可能就是不寻常的,需要再三审视。
使用平方和法可以取得很好的效果,但在处理现实世界的多样性时,要求在期望值附近的残差呈正态分布以及方差恒定的假设是有限制的。为了使用正态分布以外的概率密度分布和非恒定方差,我们应该转而使用最大似然法。
4.5 最大似然
在 R 中使用似然比较简单,因为有许多概率密度函数(PDF)的内置函数以及一系列定义其他 PDF 的软件包。再重复一遍,最大似然法的目的是使用软件搜索模型参数集,使观测数据的总似然最大化。要使用这一最优模型拟合标准,需要对模型进行定义,以便将每个观测值(可用数据)的概率或似然值指定为模型中参数值和其他变量的函数( 公式 4.2 和 公式 4.11 )。重要的是,这种规范包括对所选 PDF 的变异性或扩散性的估计(正态分布中的 \(\sigma\) 只是最小二乘法的副产品)。使用最大似然法的一个主要优点是,残差结构或关于数据预期中心倾向的观测值的预期分布不一定是正态分布。如果可以定义概率密度函数 (PDF),则可以在最大似然法框架中使用;有关许多有用概率密度函数的定义,请参见 Forbes et al, (2011)。
4.5.1 简要示例
我们将使用众所周知的正态分布来说明这些方法,然后扩展该方法以包含一系列可选的 PDF。对于数据模型拟合而言,每个PDF的主要意义在于定义单个观测值的概率密度或似然值。对于平均期望值为 \(\bar x\) 或 \(\mu\) 的正态分布,给定单个值 \(x_i\) 的概率密度或似然定义为:
\[ L\left( {x_i}|\mu_{i} ,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}{{e}^{\left( \frac{-{{\left( {x_i}-\mu_{i} \right)}^{2}}}{2\sigma^2 } \right)}} \qquad(4.11)\]
其中 \(\sigma\) 为与 \(\mu_i\) 相关的标准差。这确定了最小二乘法和最大似然方法之间的直接区别,在后者中,需要一个 PDF 的完整定义,在正态分布的情况下,它包括对均值估计 \(\mu\) 周围残差的标准偏差的显式估计。这样的估计不需要最小二乘,虽然很容易从 SSQ 值中得到。
例如,我们可以从正态分布中生成一个观测样本(参见?rnorm),然后计算该样本的均值和标准差,并比较给定的样本值与 rnorm 函数中使用的原始均值和标准差的参数估计值的可能性有多大( 表 4.1 ):
代码
# Illustrate Normal random likelihoods. see Table 4.1
set.seed(12345) # make the use of random numbers repeatable
x <- rnorm(10,mean=5.0,sd=1.0) # pseudo-randomly generate 10
avx <- mean(x) # normally distributed values
sdx <- sd(x) # estimate the mean and stdev of the sample
L1 <- dnorm(x,mean=5.0,sd=1.0) # obtain likelihoods, L1, L2 for
L2 <- dnorm(x,mean=avx,sd=sdx) # each data point for both sets
result <- cbind(x,L1,L2,"L2gtL1"=(L2>L1)) # which is larger?
result <- rbind(result,c(NA,prod(L1),prod(L2),1)) # result+totals
rownames(result) <- c(1:10,"product")
colnames(result) <- c("x","original","estimated","est > orig")
knitr::kable(result) | x | original | estimated | est > orig | |
|---|---|---|---|---|
| 1 | 5.585529 | 0.3360953 | 0.3320130 | 0 |
| 2 | 5.709466 | 0.3101778 | 0.2868818 | 0 |
| 3 | 4.890697 | 0.3965663 | 0.4901017 | 1 |
| 4 | 4.546503 | 0.3599578 | 0.4536973 | 1 |
| 5 | 5.605887 | 0.3320438 | 0.3246562 | 0 |
| 6 | 3.182044 | 0.0764269 | 0.0574370 | 0 |
| 7 | 5.630099 | 0.3271127 | 0.3158617 | 0 |
| 8 | 4.723816 | 0.3840136 | 0.4827694 | 1 |
| 9 | 4.715840 | 0.3831564 | 0.4819139 | 1 |
| 10 | 4.080678 | 0.2614493 | 0.3073533 | 1 |
| product | NA | 0.0000048 | 0.0000089 | 1 |
表 4.1 的最下面一行包含每列似然值的乘积(使用R函数 prod() 求得)。毫不奇怪,当我们使用样本的均值和标准差估计(估计,L2)而不是原始值的 mean=5 和 sd=1.0 (原始,L1)时,求得最大似然,即 \(8.9201095^{-6} > 4.7521457 ^{-6}\)。在本例中,我可以确定这些值,因为在代码开始时使用了R函数 set.seed() ,以便在特定位置启动伪随机数生成器。如果你通常使用 set.seed(),不会重复使用相同的旧序列,例如 \(12345\),因为您可能会破坏伪随机数是随机数序列的良好近似值的想法,也许可以使用 getseed()来提供合适的种子数。
因此,rnorm() 函数提供了由均值和标准差确定分布中的伪随机数,dnorm() 函数提供了观测值在均值和标准差条件下的概率密度或似然(相当于 公式 4.11 )。累积概率密度函数(cdf)由函数 pnorm() 提供,量化值由 qnorm() 确定。平均值自然具有最大的似然。还要注意的是,正态曲线是围绕均值对称的。
代码
x = 0.0 Likelihood = 0.3989423 x = 1.95996395 Likelihood = 0.05844507 x =-1.95996395 Likelihood = 0.05844507 x = 0.0 cdf = 0.5 x = 0.6744899 cdf = 0.75 x = 0.75 Quantile = 0.6744898 x = 1.95996395 cdf = 0.975 x =-1.95996395 cdf = 0.025 x = 0.975 Quantile = 1.959964 代码
# try x <- seq(-5,5,0.2); round(dnorm(x,mean=0.0,sd=1.0),5) 我们可以看到,单个似然值可能是相对较大的数字,但当它们相乘时,很快就会变成相对较小的数字。当观测数据的数量增加时,就会出现误差。即使只有十个数字,当我们将所有单个似然值相乘(使用 prod())时,结果也会很快变得非常小。如果使用与 表 4.1 中的十个数字类似的另外十个数字,总似然很容易降到 \(1e-11\) 或 \(1e-12\)。随着观察次数的增加,出现四舍五入错误的几率(即使在 64 位计算机上)也开始增加。与其将许多小数相乘得到一个极小的数,不如将这些小数相乘的标准解决方案是对似然值进行自然对数变换,然后相加。最大化对数变换似然值之和与最大化单个似然值之积一样,都能获得最佳参数。此外,许多软件中的优化器似乎都是为了最有效地最小化某个函数而设计的。简单的解决方案是,我们不最大化单个似然的乘积,而是最小化负对数似然的总和(-veLL 或 negLL())。
4.6 正态分布的似然
概率似乎是一种相当奇怪的生物。当它们来自连续的概率密度函数(PDFs)时,尽管它们具有许多相同的属性,但严格来说它们并不是概率(Edwards,1972 )。严格来讲,它们与概率密度函数下某一点的概率密度有关。根据概率的定义,整条曲线下的面积总和必须为 1.0,但连续概率密度函数任何一点下的面积都会变得无穷小。正态似然的定义使用 公式 4.11 ),而累积密度函数为:
\[ {cdf}=1=\int\limits_{x=-\infty }^{\infty }{\frac{1}{\sigma \sqrt{2\pi }}}{{e}^{\left( \frac{-{{\left( x-\mu \right)}^{2}}}{2{{\sigma }^{2}}} \right)}} \qquad(4.12)\]
我们可以使用 dnorm() 和 pnorm() 计算似然和累积密度函数(cdf)( 图 4.5 )。
代码
# Density plot and cumulative distribution for Normal Fig 4.5
x <- seq(-5,5,0.1) # a sequence of values around a mean of 0.0
NL <- dnorm(x,mean=0,sd=1.0) # normal likelihoods for each X
CD <- pnorm(x,mean=0,sd=1.0) # cumulative density vs X
plot1(x,CD,xlab="x = StDev from Mean",ylab="Likelihood and CDF")
lines(x,NL,lwd=3,col=2,lty=3) # dashed line as these are points
abline(h=0.5,col=4,lwd=1) 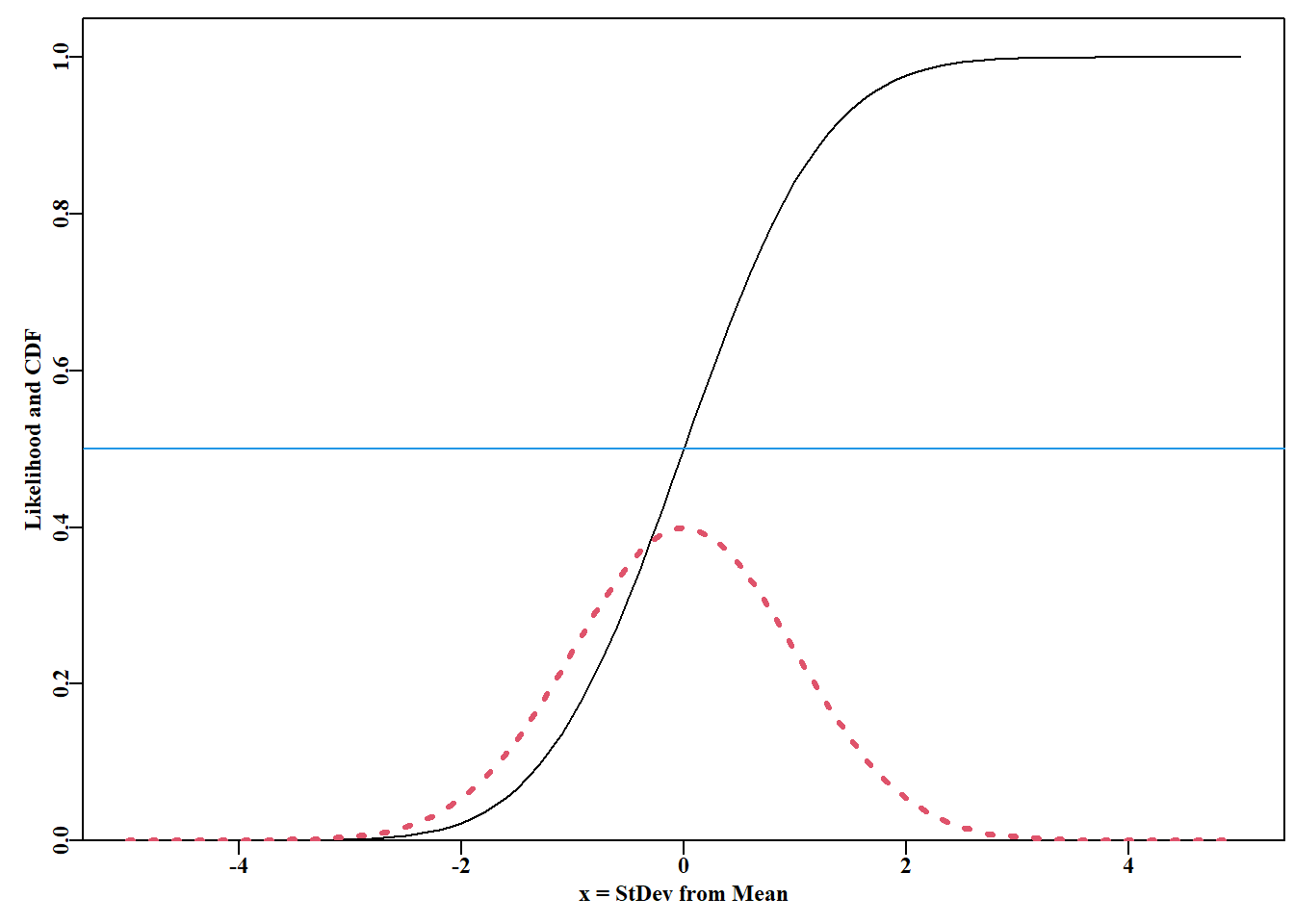
这听起来不错,但在这样的曲线下, \(x\) 变量的特定值来说,确定这样一条曲线下的特定值意味着什么呢?在 图 4.5 中,我们用虚线表示图中的似然是局部估计,不构成连续的线。每个都表示在给定 \(x\) 值处的似然。如前所述,对于 \(mean= 0.0\) 和 \(stdev = 1.0\) 的分布,在 \(0.0\) 值处的概率密度为 \(0.3989423\)。让我们简单地查看一下似然和概率之间可能存在的混淆。如果我们考虑概率密度函数的一小部分,在 \(x = 3.4\) 到 \(3.6\)的值之间 \(mean= 5.0\),\(st.dev = 1.0\) 的概率密度函数,我们可能会看到类似 图 4.6 的情况:
代码
#function facilitates exploring different polygons Fig 4.6
plotpoly <- function(mid,delta,av=5.0,stdev=1.0) {
neg <- mid-delta; pos <- mid+delta
pdval <- dnorm(c(mid,neg,pos),mean=av,sd=stdev)
polygon(c(neg,neg,mid,neg),c(pdval[2],pdval[1],pdval[1],
pdval[2]),col=rgb(0.25,0.25,0.25,0.5))
polygon(c(pos,pos,mid,pos),c(pdval[1],pdval[3],pdval[1],
pdval[1]),col=rgb(0,1,0,0.5))
polygon(c(mid,neg,neg,mid,mid),
c(0,0,pdval[1],pdval[1],0),lwd=2,lty=1,border=2)
polygon(c(mid,pos,pos,mid,mid),
c(0,0,pdval[1],pdval[1],0),lwd=2,lty=1,border=2)
text(3.395,0.025,paste0("~",round((2*(delta*pdval[1])),7)),
cex=1.1,pos=4)
return(2*(delta*pdval[1])) # approx probability, see below
} # end of plotpoly, a temporary function to enable flexibility
#This code can be re-run with different values for delta
x <- seq(3.4,3.6,0.05) # where under the normal curve to examine
pd <- dnorm(x,mean=5.0,sd=1.0) #prob density for each X value
mid <- mean(x)
delta <- 0.05 # how wide either side of the sample mean to go?
parset() # a pre-defined MQMF base graphics set-up for par
ymax <- getmax(pd) # find maximum y value for the plot
plot(x,pd,type="l",xlab="Variable x",ylab="Probability Density",
ylim=c(0,ymax),yaxs="i",lwd=2,panel.first=grid())
approxprob <- plotpoly(mid,delta) #use function defined above 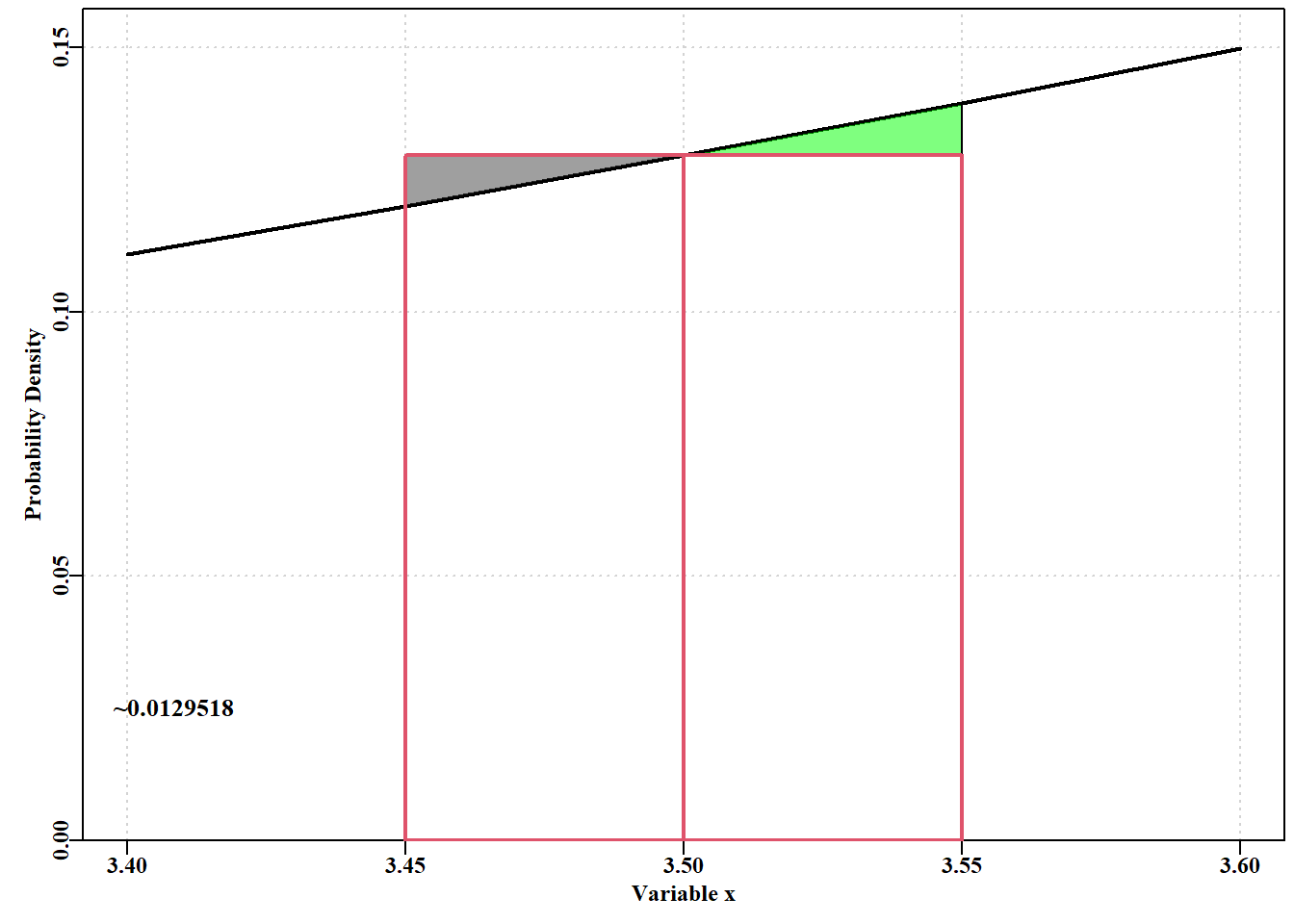
完整概率密度函数( PDF) 下的面积总和为 1.0,因此得到 图 4.6 中 \(3.45\) 和 \(3.55\) 之间值的概率是长方形面积减去左三角形面积再加上右三角形面积之和。三角形几乎是对称的,因此可以近似地相互抵消,所以近似解法就是将其中一个长方形的面积乘以 \(2.0\)。当 delta(长方形在 \(x\) 轴上的宽度)为 \(0.05\) 时,概率 \(= 0.0129518\)。如果将 delta 值改为 \(0.01\),那么近似概率 \(= 0.0025904\),随着 delta 值的减小,总概率也随之减小,尽管 \(3.5\) 时的概率密度仍为 \(0.1295176\)。显然,似然值与连续 PDF 中的概率并不相同(见 Edwards, 1972)。曲线下面积概率的最佳估计值为 pnorm(3.55,5,1) - pnorm(3.45,5,1),即 = 0.0129585。
4.6.1 与平方和等价性
当使用正态似然来拟合数据模型时,我们实际做的是设置,使得每个可用观测值的负对数似然之和最小化。幸运的是,我们可以使用dnorm()来估计似然。事实上,如果我们使用正态分布残差或对数变换的对数正态分布数据使用极大似然方法拟合模型,则得到的参数估计与使用最小二乘法得到的参数估计相同(参见下文 公式 4.19 的推导和形式)。拟合模型需要生成一组预测值 \(\hat x\) (x-hat),为其他自变量 \(\theta(x)\) 的函数,其中 \(\theta\) 是函数关系中使用的参数列。\(n\) 个观测值的对数似然定义为:
\[ LL(x|\theta)=\sum\limits_{i=1}^{n}{log\left( \frac{1}{\hat{\sigma }\sqrt{2\pi }}{{e}^{\left( \frac{-{{\left( {x_i}-{{\hat{x}}_{i}} \right)}^{2}}}{2{{{\hat{\sigma }}}^{2}}} \right)}} \right)} \qquad(4.13)\]
\(LL(x|\theta)\) 读作给定 \(\theta\) 个参数(\(\mu\) 和 \(\hat \sigma\))时观测值 \(x\) 的对数似然;符号”|“读作”给定”。这个看似复杂的方程式其实可以大大简化。首先,我们可以将指数项之前的常数移到求和项之外,乘以 \(n\) ,然后将剩余指数项的自然对数反变换为指数:
\[ LL(x|\theta)=n \log\left( \frac{1}{\hat{\sigma }\sqrt{2\pi }} \right)+\frac{1}{2{\hat{\sigma }^{2}}}\sum\limits_{i=1}^{n}{\left( -{{\left( x_i-\hat{x}_i \right)}^{2}} \right)} \qquad(4.14)\]
\(\hat \sigma^2\) 是数据方差的最大似然估计(记住是除以 \(n\) 而非 \(n-1\)):
\[ {{\hat{\sigma }}^{2}}=\frac{\sum\limits_{i=1}^{n}{{{\left( x_i-\hat{x}_i \right)}^{2}}}}{n} \qquad(4.15)\]
如果用 公式 4.15 中 \(\hat \sigma^2\) 代入 公式 4.14 ,则 \((x_i-\hat x_i)^2\) 用 \(-n/2\) 代替:
\[ LL(x|\theta)=n{\log}\left( \left( {\hat{\sigma }\sqrt{2\pi }} \right)^{-1} \right) - \frac{n}{2} \qquad(4.16)\]
化简平方根意味着将 \(- 1\) 移至对数项外面,\(n\) 变成 \(- n\),我们可以将平方根变成指数 \(1/2\),然后将 \(\log(\hat \sigma)\) 项加到 \(\pi\) 项上:
\[ LL(x|\theta)=-n\left( {\log}\left( {{\left( 2\pi \right)}^{\frac{1}{2}}} \right)+{\log}\left( {\hat{\sigma }} \right) \right)-\frac{n}{2} \qquad(4.17)\]
将幂指数 \(1/2\) 移到第1个 log 项外:
\[ LL(x|\theta)=-\frac{n}{2}\left( {\log}\left( 2\pi \right)+2{\log}\left( {\hat{\sigma }} \right) \right)-\frac{n}{2} \qquad(4.18)\]
然后将 \(n/2\) 简化,并将整个方程两边乘以 \(- 1\),以转换为负对数似然,从而得到正态分布值的负对数似然的最终简化:
\[ -LL(x|\theta)=\frac{n}{2}\left( {\log}\left( 2\pi \right) + 2{\log} \left( {\hat{\sigma }} \right) + 1 \right) \qquad(4.19)\]
其中唯一的非常数部分是 \(\hat \sigma\) 的值,它是残差平方和除以 \(n\) 的平方根,所以现在应该很清楚了,为什么使用最大似然时获得的参数,如果使用正态随机误差,与从最小二乘方法得到的参数相同。
4.6.2 应用正态似然拟合数据模型
我们可以使用数据集 LatA 中的模拟雌性红鱼数据重复这个例子,图,
我们可以使用数据集 LatA中的模拟雌性红鱼数据来重复这个例子( 图 4.7 ),我们用它来说明平方残差之和的使用。理想情况下,我们应该得到相同的答案,但估计值为 \(\sigma\) 的估计值。MQMF 函数 plot1() 只是绘制单个图形(type=“l”或 type=“p”;请参阅 ?plot1)的一种快速方法,没有太多空白。如果你比我更喜欢空白,请编辑 plot1()!
代码
现在,我们可以使用 MQMF 函数 negNLL()(负正态对数似然值)以确定使用正态随机误差的负对数似然值之和(negLL()对对数正态分布数据也有同样的作用)。如果你查看一下 negNLL() 的代码,就会发现它与 ssq() 一样,都是将一个函数作为参数传递给它,然后用它来计算每个输入年龄的预测平均值(在本例中是使用 MQMF 函数 vB()计算的年龄长度),然后使用 dnorm() 以预测值作为平均值,并使用数据中的年龄-长度观测值来计算 -veLL 之和。年龄数据是通过省略号(…)传递的,并没有在 negNLL() 中明确声明为参数。该函数在结构上与 ssq() 非常相似,输入要求完全相同,但 pars 是显式传递的,而不是在…中传递,因为 pars 的最后一个值必须是残差的 stdev,它将在 negNLL() 中使用,而不只是在 funk 中使用。因此,negNLL()的运行方式与ssq()非常相似,它是调用函数生成预测值的封装程序,然后使用 dnorm() 在每次调用时返回一个数字。因此,nlm() 会最小化 negNLL(),而 negNLL() 又会调用 vB()。
代码
# Fit the vB growth curve using maximum likelihood
pars <- c(Linf=27.0,K=0.15,t0=-3.0,sigma=2.5) # starting values
# note, estimate for sigma is required for maximum likelihood
ansvB <- nlm(f=negNLL,p=pars,funk=vB,observed=lengths,ages=ages,
typsize=magnitude(pars))
outfit(ansvB,backtran=FALSE,title="vB by minimum -veLL") nlm solution: vB by minimum -veLL
minimum : 747.0795
iterations : 26
code : 1 gradient close to 0, probably solution
par gradient
1 26.8354474 4.490629e-07
2 0.1301554 1.659593e-05
3 -3.5868868 2.852562e-07
4 1.9500896 8.278354e-06如果回顾一下 von Bertalanffy 曲线的 ssq() 例子,你会看到我们从358尾鱼的样本中得到SSQ值为 \(1361.421\) (试试 nrow(LatA))。因此 ssq() 方法对 \(\sigma\) 的估计值为 \(\sqrt{(1361.421/358)}=1.95009\),与预期的最大似然估计基本相同。
和以前一样,我们所需要做的就是把一个不同的生长曲线函数代入 negNLL() 就可得到结果。我们只需要记住在 \(p\) 向量中包含第四个参数(\(\sigma\) )。同样,使用正态随机误差得到的数值解与使用 ssq() 方法得到的数值解本质上是相同的。
代码
nlm solution: MM by minimum -veLL
minimum : 743.6998
iterations : 34
code : 1 gradient close to 0, probably solution
par gradient
1 20.7464280 -6.195246e-06
2 1.4183165 1.601881e-05
3 0.9029899 2.461309e-04
4 1.9317669 -3.359816e-06同样,解决方案的梯度很小,这增加了解决方案不仅仅是局部最小值的信心,所以我们应该画出解决方案,看看它与数据的相对拟合。
通过在数据点上绘制拟合曲线,数据不会遮挡线条。现在可以从该分析中产生的实际预测,也可以与残值一起制成表格。通过包含单个残差的平方,可以更清楚地看出哪些点(见记录3)可能具有最大的影响。
代码
#plot optimum solutions for vB and mm. Fig 4.8
Age <- 1:max(ages) # used in comparisons
predvB <- vB(ansvB$estimate,Age) #optimum solution
predMM <- mm(ansMM$estimate,Age) #optimum solution
parset() # plot the deata points first
plot(ages,lengths,xlab="Age",ylab="Length",type="p",pch=16,
ylim=c(10,33),panel.first=grid(),col=rgb(1,0,0,1/3))
lines(Age,predvB,lwd=2,col=4) # then add the growth curves
lines(Age,predMM,lwd=2,col=1,lty=2)
legend("bottomright",c("von Bertalanffy","Michaelis-Menton"),
col=c(4,1),lwd=3,bty="n",cex=1.2,lty=c(1,2)) 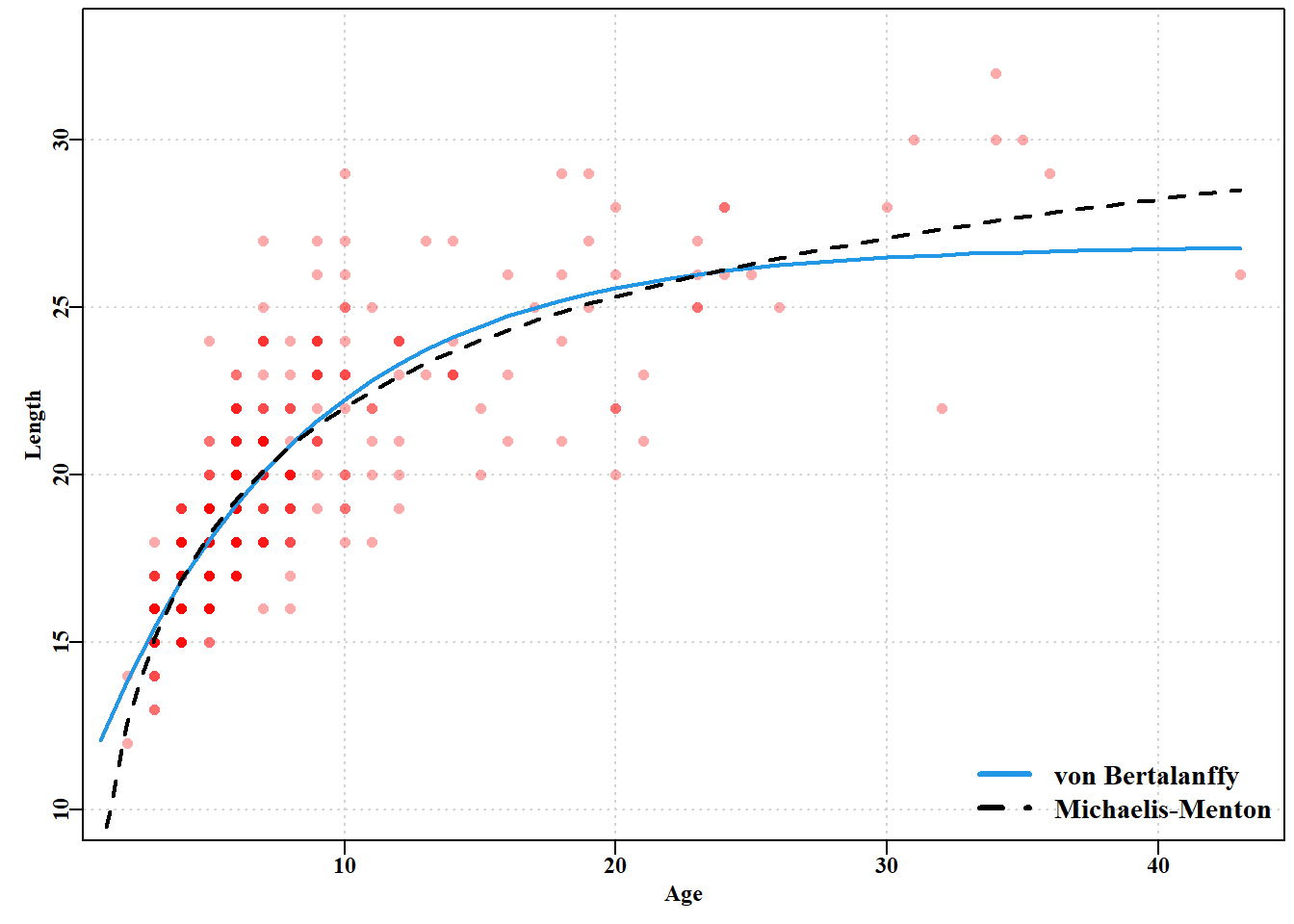
通常,我们会生成残差图来检查残差特征( 图 4.9 )。
代码
# residual plot for vB curve Fig 4.9
predvB <- vB(ansvB$estimate,ages) # predicted values for age data
resids <- lengths - predvB # calculate vB residuals
plot1(ages,resids,type="p",col=rgb(1,0,0,1/3),xlim=c(0,43),
pch=16,xlab="Ages Years",ylab="Residuals")
abline(h=0.0,col=1,lty=2) # emphasize the zero line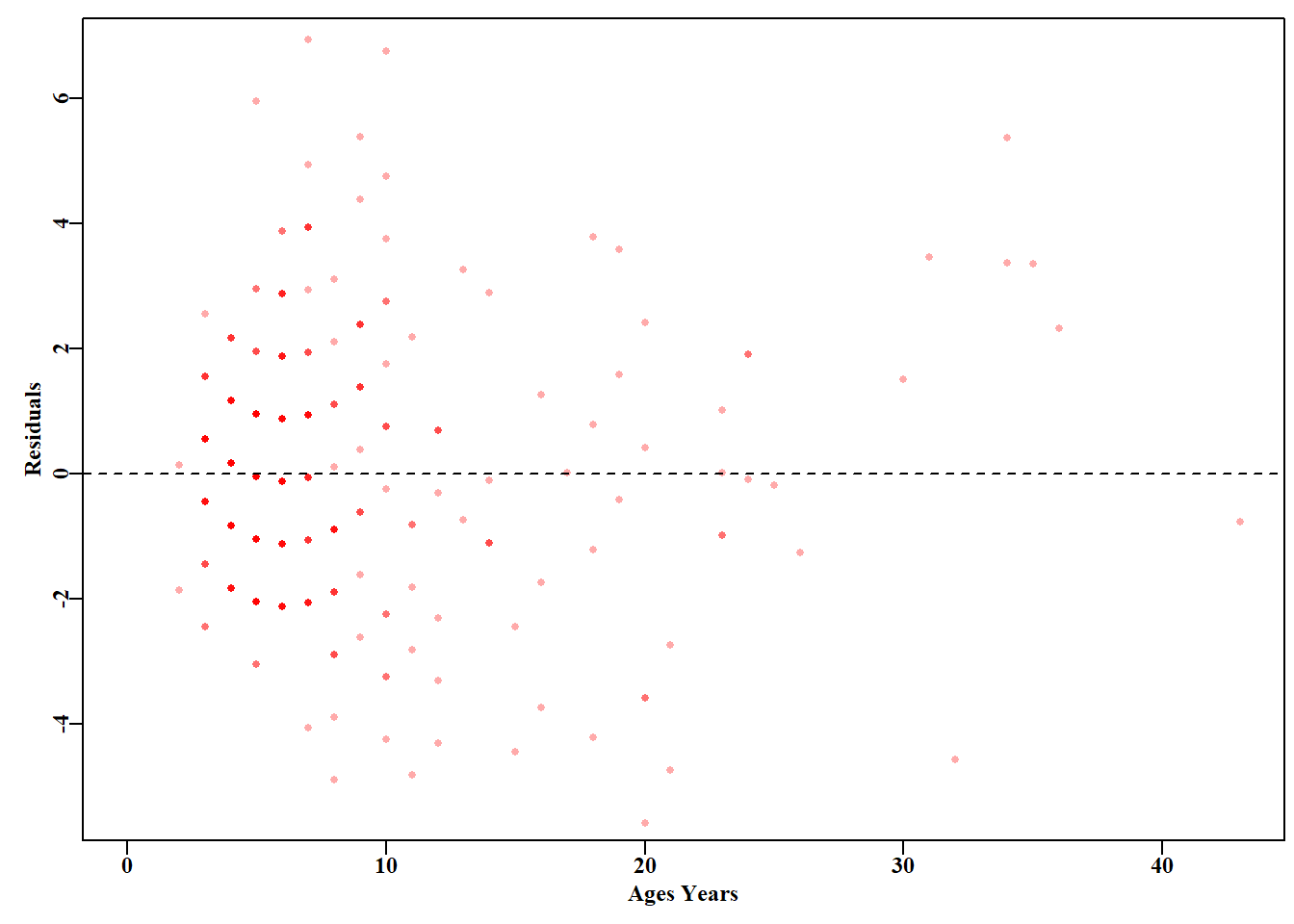
生长数据的图(图 4.8 和 图 4.9 )中,数据的网格性质清楚地表明测量的长度精确到厘米,年龄四舍五入到最接近的整年。在 x 轴和 y 轴上的这种舍入与我们用经典的 y-on-x 方法拟合这些模型的问题相结合(Ricker, 1973),并且假设在 x 轴上的测量没有变化,但不幸的是,与年龄有关,这个假设是完全错误的。从本质上讲,我们将长度和年龄的变量视为离散的,而不是连续的,年龄数据是精确的,没有误差。这些特征值得进一步探索,但也有助于强调,当处理来自生活世界的数据时,很难收集,而且通常我们处理的信息并不完美。在渔业和现实世界的生态学中建立模型的真正诀窍是从那些不太完美的数据中获得有用和有趣的信息,并以一种站得住的方式这样做。
4.7 对数正态似然
正态分布具有高于或低于预期平均值的加性残差误差,这是众所周知的,其特性构成了许多有关自然的直觉的基础。然而,在开发种群中发现的许多变量(CPUE、渔获量、努力量……)都呈现出高度倾斜的分布,中心倾向并不位于分布的中心(正态分布就是这样)。对数正态分布(Log-Normal distribution)是用于描述此类数据的一种非常常见的 PDF 分布:
\[ L\left( x_i|m_i ,\sigma \right)=\frac{1}{{x_i}\sigma \sqrt{2\pi }}{{e}^{\left( \frac{-{{\left(\log{(x_{i})}-\log{(m_i)} \right)}^{2}}}{2\sigma^2 } \right)}} \qquad(4.20)\]
其中, \(L(x_i | m, \sigma\) 为数据点 \(x_i\) 的似然,\(m_i\) 为 \(i\) 点变量实例的中位数,\(m= e^{\mu}\) ( \(\mu = \log(m)\) )。用 \(\log(x)\) 的均值估算 \(\mu\),\(\sigma\) 是 \(\log(x)\) 的标准差。
对数正态似然方程(公式 4.20 )在视觉上与正态分布相似,不同之处在于对数正态分布的残差是乘性的,而不是加性的。详细地说,每个似然乘以观测值的倒数,观测值和期望值进行对数变换。具体上讲,每个似然乘以观测值的倒数,观测值和期望值进行对数变换。对观测数据和期望值的对数变换意味着,我们不是使用 \(x_i-m_i\) 的变量,而是使用等价的 \(x_i/m_i\) 计算残差。这意味着观测值除以预期值,而不是从观测值中减去预期值。所有这些残差都将是正值,并将围绕 1.0 的值变化。残差为 1.0 意味着数据点完全符合该数据点的预期中值。
4.7.1 对数正态似然的简化
与正态似然一样,对数正态似然也可以简化,以方便后续计算:
\[ -LL(x|\theta)=\frac{n}{2}\left( {\log}\left( 2\pi \right)+2{\log}\left( {\hat{\sigma }} \right) + 1 \right)+\sum\limits_{i=1}^{n}{{\log}\left( {{x}_{i}} \right)} \qquad(4.21)\]
\(\hat \sigma^2\) 的最大似然估计是:
\[ {{\hat{\sigma }}^{2}}=\sum\limits_{i=1}^{n}{\frac{{{\left( log\left( {{x}_{i}} \right)-log\left( {{{\hat{x}}}_{i}} \right) \right)}^{2}}}{n}} \qquad(4.22)\]
再次注意方差的最大似然估计用 \(n\) 而非 \(n-1\)。 公式 4.21 末尾的 \(\sum \log(x)\) 项是常量,在拟合模型时经常忽略掉。如上所述,假设我们忽略 \(\sum \log(x)\) 项,那么 公式 4.22 似乎与正态分布相同( 公式 4.13 )。然而,现在 \(\sigma\) 需要将观测值和预测值进行对数转换( 公式 4.22 )。因此,只要在分析前对数据和预测值进行对数变换,我们就可以使用与正态似然相关的函数(如 negNLL())来拟合使用对数正态残差的模型。不过,一般情况下,我们会使用 negLL(),它需要对数变换的观测值和一个生成预测值对数的函数(见 ?negLL)。
4.7.2 对数正态分布的性质
对于正态分布,我们知道分布的期望均值、中位数和模都是相同的,但对于对数正态分布,情况并非如此。给定一组连续变量 \(x\) 的值,其中位数的估计值为
\[ \text{median} =m = e^{\mu} \qquad(4.23)\]
其中 \(\mu\) 是 \(\log(x)\) 的均值,对数正态分布的模定义为:
\[ \text{mode} = \dfrac{m}{e^{\sigma^2}}=e^{(\mu-\sigma^2)} \qquad(4.24)\]
其中 \(\sigma\) 是 \(\log(x)\) 的标准差。最终,对数正态分布的均值或期望值定义为:
\[ \bar{x} = me^{(\sigma^2/2)} = e^{(\mu + \sigma^2/2)} \qquad(4.25)\]
这些方程( 公式 4.23 到 公式 4.25 ) 表明对数正态分布总是右斜(在模的右侧有一长尾)。此外,与正态分布相比,对数正态分布仅定义了 \(x\) 为正值的情形,见 图 4.10 。
代码
# meanlog and sdlog affects on mode and spread of lognormal Fig 4.10
x <- seq(0.05,5.0,0.01) # values must be greater than 0.0
y <- dlnorm(x,meanlog=0,sdlog=1.2,log=FALSE) #dlnorm=likelihoods
y2 <- dlnorm(x,meanlog=0,sdlog=1.0,log=FALSE)#from log-normal
y3 <- dlnorm(x,meanlog=0,sdlog=0.6,log=FALSE)#distribution
y4 <- dlnorm(x,0.75,0.6) #log=TRUE = log-likelihoods
parset(plots=c(1,2)) #MQMF shortcut plot formatting function
plot(x,y3,type="l",lwd=2,panel.first=grid(),
ylab="Log-Normal Likelihood")
lines(x,y,lwd=2,col=2,lty=2)
lines(x,y2,lwd=2,col=3,lty=3)
lines(x,y4,lwd=2,col=4,lty=4)
legend("topright",c("meanlog sdlog"," 0.0 0.6",
" 0.0 1.0"," 0.0 1.2"," 0.75 0.6"),
col=c(0,1,3,2,4),lwd=3,bty="n",cex=1.0,lty=c(0,1,3,2,4))
plot(log(x),y3,type="l",lwd=2,panel.first=grid(),ylab="")
lines(log(x),y,lwd=2,col=2,lty=2)
lines(log(x),y2,lwd=2,col=3,lty=3)
lines(log(x),y4,lwd=2,col=4,lty=4) 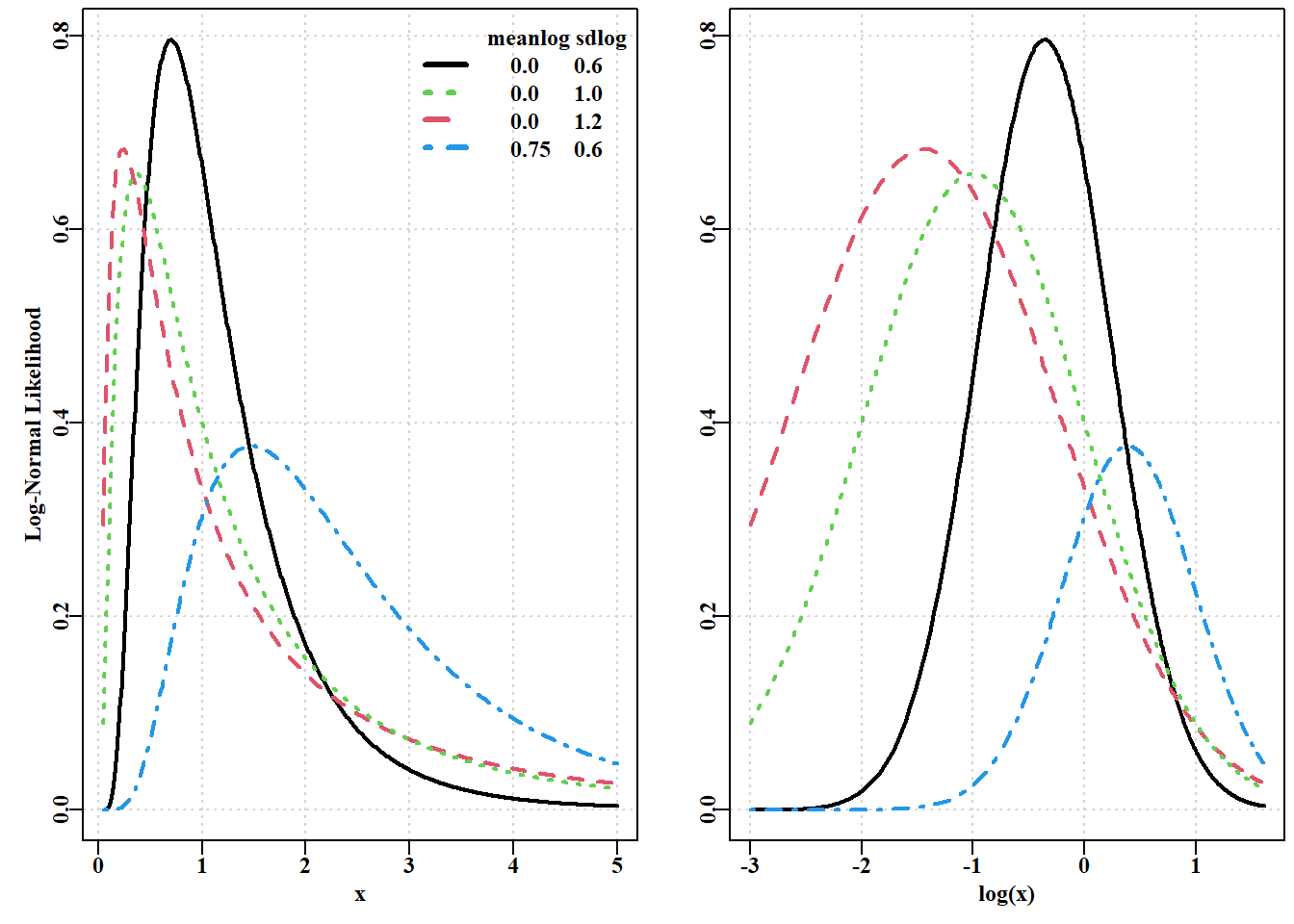
同样,可以从对数正态分布生成随机数,与之前一样,对数变换应生成正态分布, 如 图 4.11 所示。
代码
set.seed(12354) # plot random log-normal numbers as Fig 4.11
meanL <- 0.7; sdL <- 0.5 # generate 5000 random log-normal
x <- rlnorm(5000,meanlog = meanL,sdlog = sdL) # values
parset(plots=c(1,2)) # simplifies the plots par() definition
hist(x[x < 8.0],breaks=seq(0,8,0.25),col=0,main="")
meanx <- mean(log(x)); sdx <- sd(log(x))
outstat <- c(exp(meanx-(sdx^2)),exp(meanx),exp(meanx+(sdx^2)/2))
abline(v=outstat,col=c(4,1,2),lwd=3,lty=c(1,2,3))
legend("topright",c("mode","median","bias-correct"),
col=c(4,1,2),lwd=3,bty="n",cex=1.2,lty=c(1,2,3))
outh <- hist(log(x),breaks=30,col=0,main="") # approxnormal
hans <- addnorm(outh,log(x)) #MQMF function; try ?addnorm
lines(hans$x,hans$y,lwd=3,col=1) # type addnorm into the console 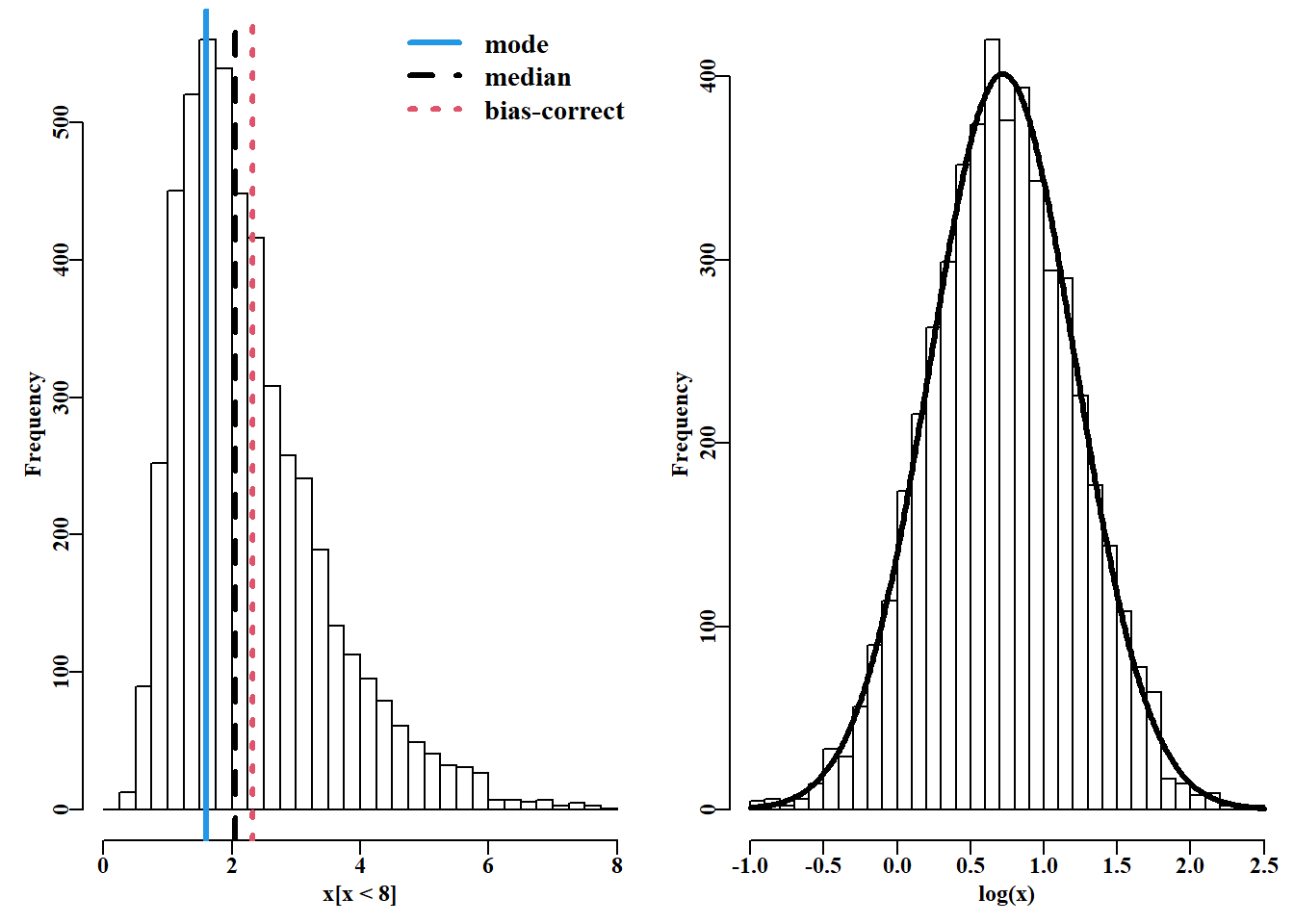
我们可以检查输入参数的预期统计量,并将其与变量 outstat 中的参数估计进行比较。
代码
#examine log-normal propoerties. It is a bad idea to reuse
set.seed(12345) #'random' seeds, use getseed() for suggestions
meanL <- 0.7; sdL <- 0.5 #5000 random log-normal values then
x <- rlnorm(5000,meanlog = meanL,sdlog = sdL) #try with only 500
meanx <- mean(log(x)); sdx <- sd(log(x))
cat(" Original Sample \n") Original Sample Mode(x) = 1.568312 1.603512 Median(x) = 2.013753 2.052606 Mean(x) = 2.281881 2.322321 代码
cat("Mean(log(x) = 0.7 ",meanx,"\n") Mean(log(x) = 0.7 0.7001096 代码
cat("sd(log(x) = 0.5 ",sdx,"\n") sd(log(x) = 0.5 0.4944283 中位数与均值之间的差异,即 \(+ (\sigma^2/2)\) 项,被称为偏差修正项,并试图通过将中心倾向的测量值进一步向右偏离模式来解释分布的向右偏斜。模似乎位于最高组的左侧,但这只是反映了 R 绘制直方图的方式(您可以增加一半的二进制宽度来解决这个视觉问题)。
4.7.3 应用对数似然拟合曲线
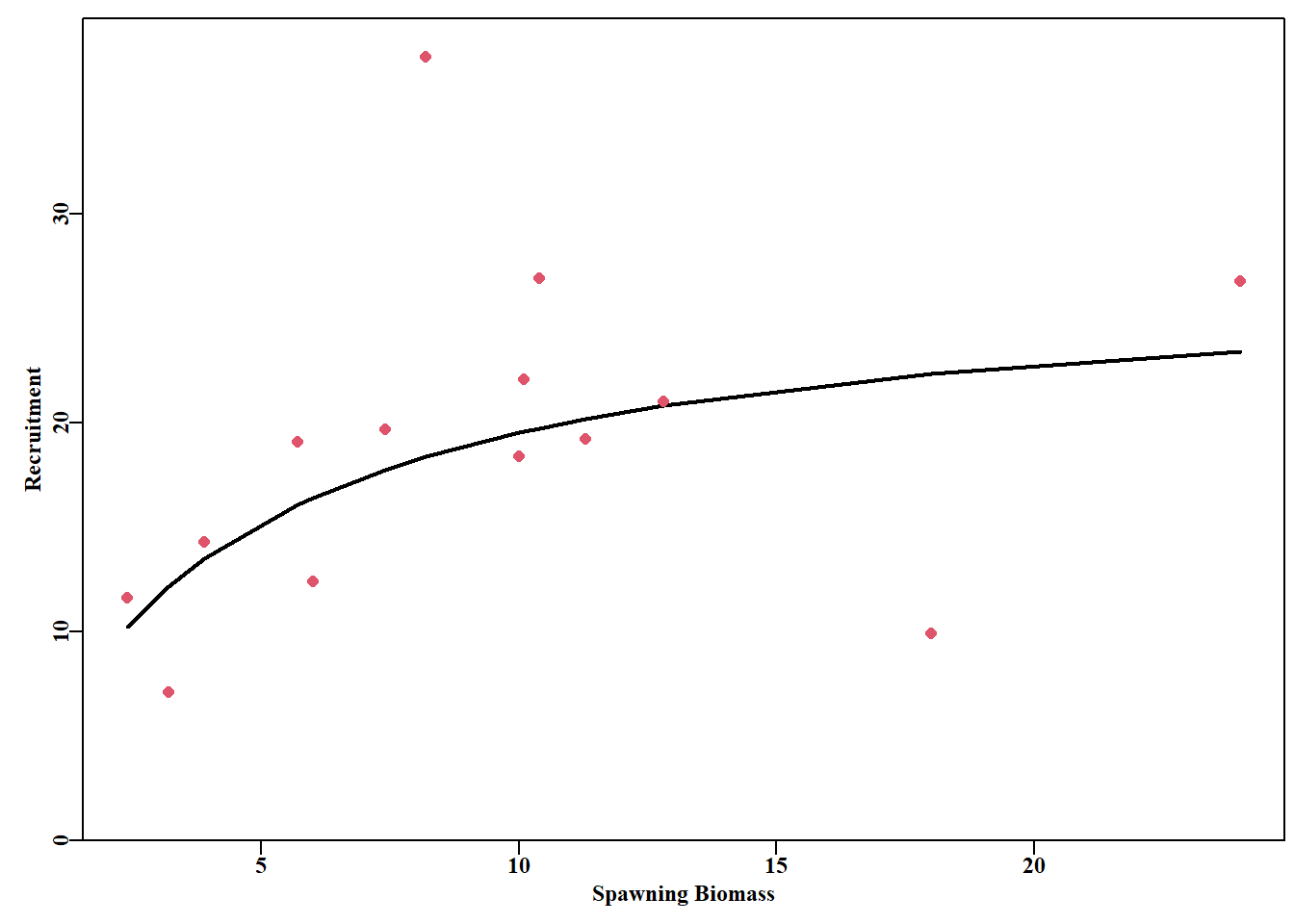
我们可以使用 Penn 和 Caputi(1986)关于澳大利亚埃克斯茅斯湾老虎虾(Penaeus semisulcatus;MQMF 数据集 tigers)的产卵种群生物量及其补充量数据。种群补充关系通常假定为对数正态残差(有时为伽马分布,见后),通常在种群评估模型中得出。Penn 和 Caputi(1986 年)使用的是 Ricker 曲线,但作为替代方案,我们将尝试根据这些观测数据拟合 Beverton-Holt 种群补充量曲线(我们将在静态模型一章中更详细地研究种群补充量关系)。Beverton-Holt 种群补充量关系可以有多种形式,但在本例中我们将使用 公式 4.26 :
\[ R_t=\frac{aB_t}{b+B_t}e^{N(0,\sigma^2)} \qquad(4.26)\]
其中 \(R_t\) 是年 \(t\) 的补充量, \(B_t\) 是繁殖亲体量,它能生产出 \(R_t\) 的补充量,\(a\) 是渐近最大补充量水平,\(b\) 是生产最大补充量的 50% 时的繁殖亲体量。残差误差是 \(\mu=0\)、方差为 \(\sigma^2\) 的对数分布,这些参数可以通过对数据进行模型拟合得到。我们将继续使用 negNLL(),但如果您检查一下 negNLL() 的代码,就会发现我们需要输入对数变换后的观测补充量水平,并编写一个简短函数来计算预测补充量水平的对数。我们将再次使用 nlm() 来最小化 negNLL() 的输出结果。当我们考虑 表 4.2 中的对数正态残差(观测补充量/预测补充量)时,注意到有两个特殊的残差值,一个接近 \(2.04\),另一个接近 \(0.44\)。低点的潜在影响可能值得进一步研究,因为它是相对特殊的事件(事实上,它似乎受到气旋发生的影响,Penn 和 Caputi,1986 )。
代码
# fit a Beverton-Holt recruitment curve to tigers data Table 4.2
data(tigers) # use the tiger prawn data set
lbh <- function(p,biom) return(log((p[1]*biom)/(p[2] + biom)))
#note we are returning the log of Beverton-Holt recruitment
pars <- c("a"=25,"b"=4.5,"sigma"=0.4) # includes a sigma
best <- nlm(negNLL,pars,funk=lbh,observed=log(tigers$Recruit),
biom=tigers$Spawn,typsize=magnitude(pars))
outfit(best,backtran=FALSE,title="Beverton-Holt Recruitment") nlm solution: Beverton-Holt Recruitment
minimum : 5.244983
iterations : 16
code : 1 gradient close to 0, probably solution
par gradient
1 27.344523 -5.109267e-08
2 4.000166 1.265602e-07
3 0.351939 1.789283e-06| SpawnB | Recruit | PredR | Residual |
|---|---|---|---|
| 2.4 | 11.6 | 10.25393 | 1.1312736 |
| 3.2 | 7.1 | 12.15284 | 0.5842256 |
| 3.9 | 14.3 | 13.49891 | 1.0593447 |
| 5.7 | 19.1 | 16.06816 | 1.1886865 |
| 6.0 | 12.4 | 16.40644 | 0.7558007 |
| 7.4 | 19.7 | 17.74969 | 1.1098783 |
| 8.2 | 37.5 | 18.37886 | 2.0403883 |
| 10.0 | 18.4 | 19.53157 | 0.9420646 |
| 10.1 | 22.1 | 19.58698 | 1.1283005 |
| 10.4 | 26.9 | 19.74859 | 1.3621223 |
| 11.3 | 19.2 | 20.19541 | 0.9507111 |
| 12.8 | 21.0 | 20.83372 | 1.0079815 |
| 18.0 | 9.9 | 22.37262 | 0.4425051 |
| 24.0 | 26.8 | 23.43802 | 1.1434411 |
我们可以绘制出解,直观地比较数据拟合结果:
代码
4.7.4 应用对数正态误差拟合动态模型
本例中,我们将回顾第 7 章“剩余产量模型 ”中的一个例子(并在第 3 章“简单种群模型 ”中查看)。具体而言,我们将使用所谓的Schaefer(1954,1957)剩余产量模型(Hilborn 和 Walters,1992;Polacheck 等,1993;Prager,1994;Haddon,2011)。用于描述 Schaefer 模型的最简单方程包含两个项:
\[ \begin{aligned} {B_0} &= {B_{init}} \\ {B_{t+1}} &= {B_t}+r{B_t}\left( 1-\frac{{B_t}}{K} \right)-{C_t} \end{aligned} \qquad(4.27)\]
其中 \(r\) 是内禀自然增长率(种群增长率项),\(K\) 是环境容纳量或未被捕捞时的生物量,一般用 \(B_0\) 表示(注意的是,这里的 \(B_0\) 简单地表示 \(t=0\) 时的初始生物量),\(B_{init}\) 可能已衰退低于 \(K\)。\(B_t\) 表示年 \(t\) 可用生物量,那么 \(B_{init}\) 是第一年中可用生物量。如果资源未被捕捞,那么 \(B_{init} =K\),但在其他情况下,它将构成一个单独的模型参数。最后, \(C_t\) 是年 \(t\) 中捕捞的总获量。当然,时间步长不必以年为单位,可能需要更短的时间,这取决于相关物种的生物学特性,不过,使用年是很常见的。注意 公式 4.27 中没有误差项。这意味着种群动态是确定的,渔获量是已知的,没有误差。估算该模型的参数就是使用观察误差估算的一个例子。
公式 4.27 中的简单动态模型,在所需参数(\(B_{init}\)、\(r\) 及 \(K\) )已知时,将初始生物量向前推算,生成种群生物量水平的时间序列。如果有相对丰度指数的时间序列(可能是调查得出的生物量估计值,也可能是渔业相关数据得出的标准化单位努力量渔获量(CPUE)),就可以将剩余产量模型与自然界的观测结果进行比较。在下面的例子中,我们将使用 MQMF 数据集 abdat 中潜水捕捞无脊椎动物的渔获量和 CPUE。假设相对丰度指数与种群生物量之间存在简单的线性关系:
\[ {I_t}=\frac{C_t}{E_t}=q{B_t}e^{\varepsilon}{ \;\;\;\;\;\; \text{or} \;\;\;\;\;\; } {C_t}=q{E_t}{B_t}e^{\varepsilon} \qquad(4.28)\]
其中 \(I_t\) 是年 \(t\) 的观测 CPUE,\(E_t\) 是年 \(t\) 的努力量, \(q\) 为可捕系数(Arreguin-Sanchez, 1996),\(e^{\varepsilon}\) 表示CPUE 和 种群生物量关系的对数正态残差误差。 该 \(q\) 可以作为一个参数直接估算,尽管也有所谓的闭合形式估算值(Polacheck 等,1993):
\[ q={e}^{\frac{1}{n}{\sum{\log}\left( \frac{{{I}_{t}}}{{{{\hat{B}}}_{t}}} \right)}}=\exp \left( {\frac{1}{n}}\sum{\log}\left( \frac{{I}_{t}}{\hat{B}_{t}} \right) \right) \qquad(4.29)\]
基本上就是观测到的 CPUE 向量的几何平均数除以预测的每年生物量水平。使用这种封闭形式的一个好处是,在拟合数据时,模型需要估计的参数较少。它还强调 \(q\) 参数只是一个比例因子,反映了可开发生物量与相对丰度指数之间的假定线性关系。如果假定存在非线性关系,则需要更复杂的可捕量表示方法。
上例中拟合的种群增殖曲线使用了一个相对简单的方程和相关函数作为拟合模型,但模型中不涉及动态变化。当试图将 公式 4.27 至 公式 4.29 中描述的剩余产量模型与观测到的 CPUE 和渔获量数据进行拟合时,得出预测 CPUE 的函数需要更加复杂,因为它需要包含种群动态。对于简单的非动态模型,自变量和因变量的使用相对简单。在此,我们将说明(并强化)在将动态模型拟合到数据时需要做哪些工作。
我们将使用名为 abdat 的 MQMF 数据集,该数据集因包含鲍鱼数据而得名。
代码
data(abdat) # plot abdat fishery data using a MQMF helper Fig 4.13
plotspmdat(abdat) # function to quickly plot catch and cpue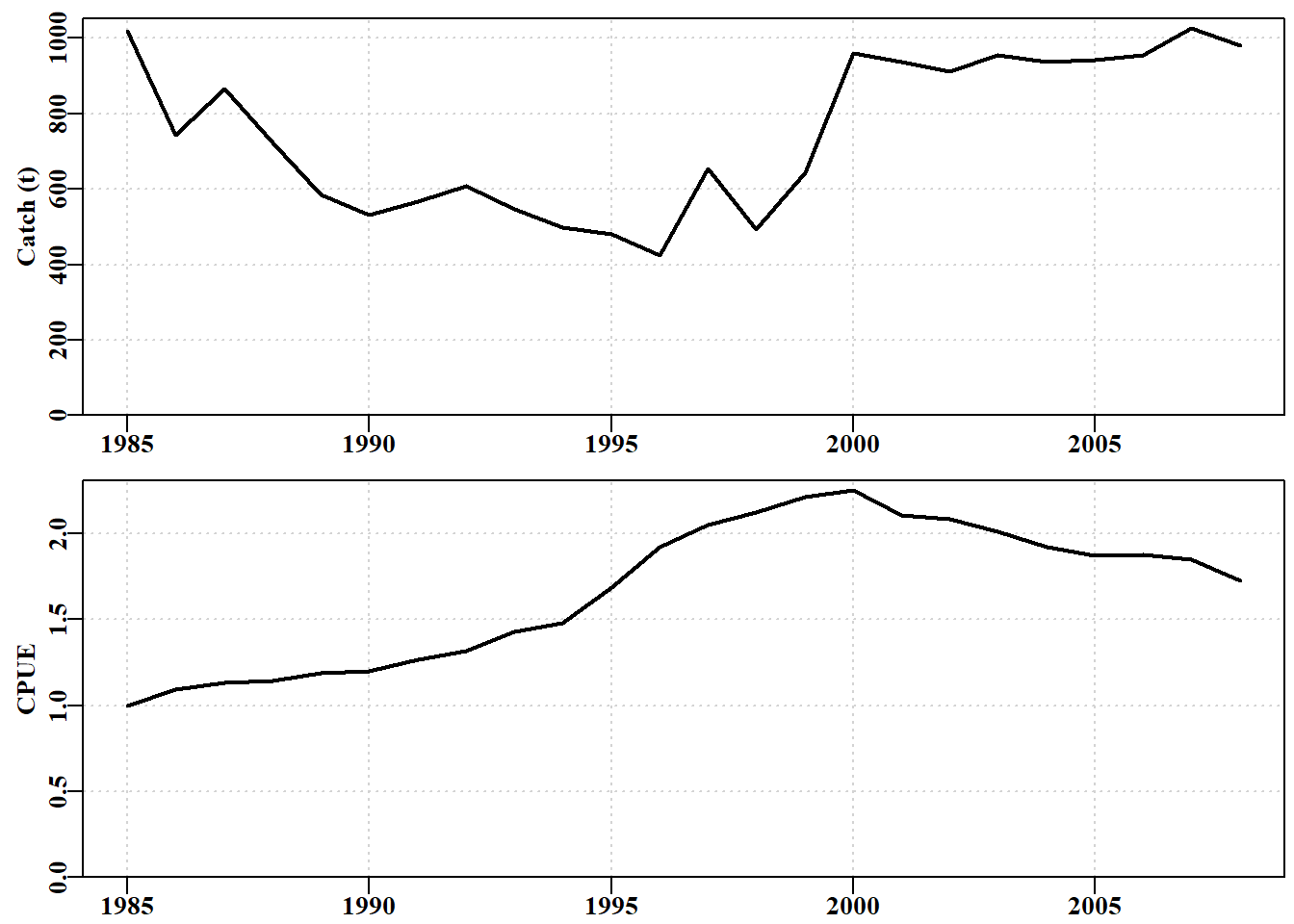
我们需要在 nlm() 中使用两个函数来找到最佳参数。您应该检查每个函数的代码,并了解它们与所用方程的关系。第一个函数用于计算预测 cpue 的对数(我们使用 simpspm()),第二个函数用于计算 -veLL,其中我们使用对数正态残差误差来表示 cpue 数据的残差(因此我们使用 negLL();将其代码与 negNLL() 进行比较)。请注意模型参数将进行对数变换的预期,我们这样做是因为它通常比使用 typsize 选项更稳定。你应该通过尝试不同的起始点来实验这段代码。你应该仔细检查 simpspm 和 negLL() 的代码,直到理解它们之间的相互作用,并相信您可以用不同的数据集重复这一分析(参见第 7 章“剩余产量模型 ” )。
代码
# Use log-transformed parameters for increased stability when
# fitting the surplus production model to the abdat data-set
param <- log(c(r= 0.42,K=9400,Binit=3400,sigma=0.05))
obslog <- log(abdat$cpue) #input log-transformed observed data
bestmod <- nlm(f=negLL,p=param,funk=simpspm,indat=as.matrix(abdat),
logobs=obslog) # no typsize, or iterlim needed
#backtransform estimates, outfit's default, as log-transformed
outfit(bestmod,backtran = TRUE,title="abdat") # in param nlm solution: abdat
minimum : -41.37511
iterations : 20
code : 2 >1 iterates in tolerance, probably solution
par gradient transpar
1 -0.9429555 6.743051e-06 0.38948
2 9.1191569 -9.223729e-05 9128.50173
3 8.1271026 1.059182e-04 3384.97779
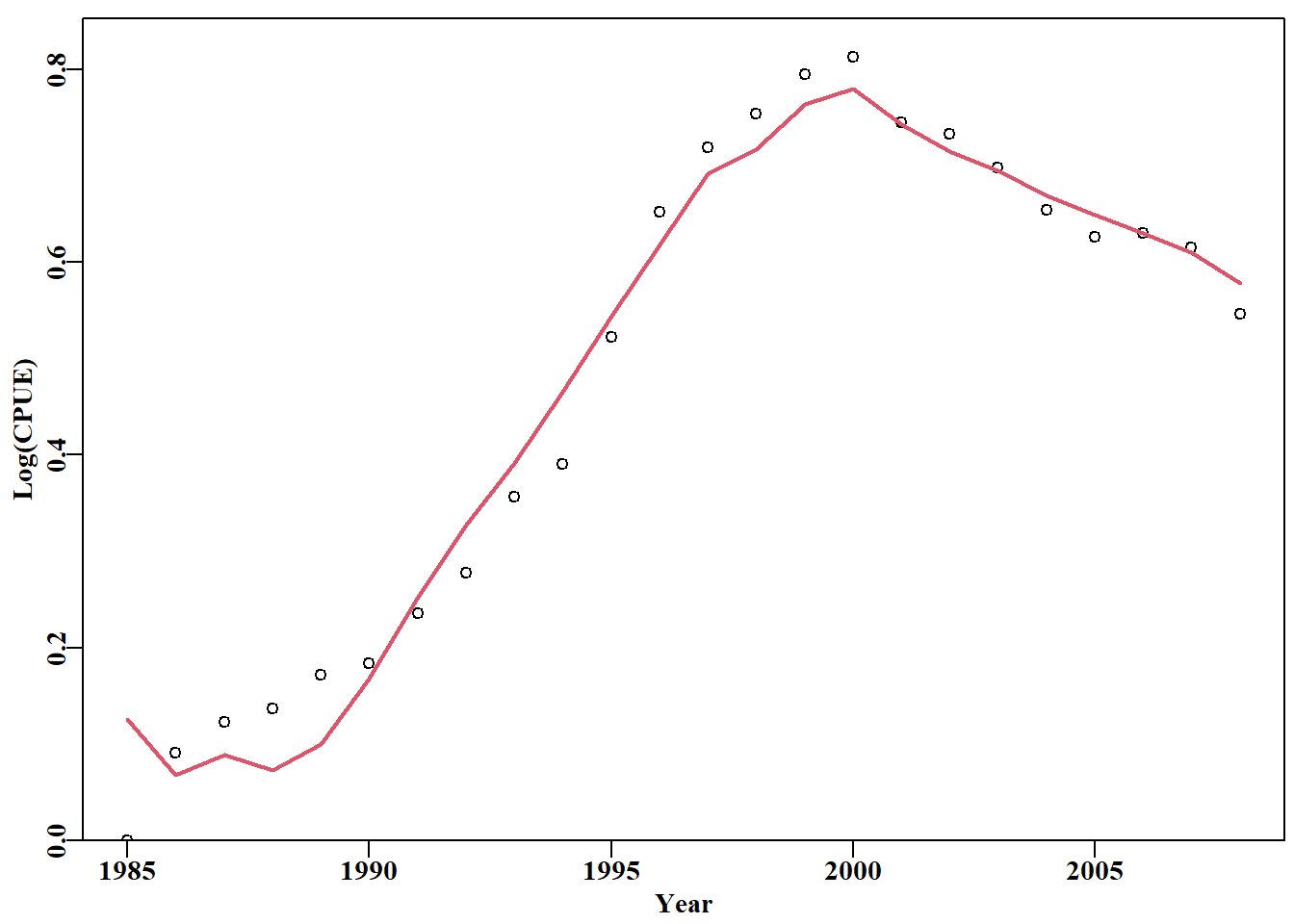
4 -3.1429030 -8.116218e-07 0.04316将观察到的数据与最优模型的预测值对比绘制成图总是一个好主意。在这里,我们将它们绘制成对数比例,以准确说明拟合结果,并帮助确定哪些点与预测值相差最大。由于很少有人能直观地掌握对数标度,因此在标称标度上绘制数据和拟合结果也是一个好主意,此外,我们通常还会绘制残差图来寻找规律。
代码
4.8 二项式分布的似然
到目前为止,通过正态分布和对数正态分布,我们一直在处理连续变量(如产卵生物量和 cpue)特定值的似然。当然,有些观测结果和事件在本质上是离散的。常见的例子包括动物是否成熟、是否有标签或类似的 “是”/“否”情况。与连续变量不同,当使用离散型分布(如二项分布)计算特定值(如在 \(n\) 个观测样本中看到 \(m\) 个标记的似然)的似然时,它们是真正的概率,而不仅仅是概率密度。这样,就避免了理解并非真实概率的似然的复杂性;这可能就是为什么许多介绍极大似然方法的文章倾向于从使用二项分布的例子开始的原因。
在观察结果有真有假的情况下(所谓伯努利试验;例如,捕获的鱼要么有标记,要么没有标记),\(n\) 次观察(试验)的成功概率为参数 \(p\),那么通常最好使用二项分布来描述观察结果。二项分布概率密度函数产生真实概率,有两个参数:\(n\),即试验次数(样本大小);\(p\),即试验成功的概率(事件/观察结果证明为真):
\[ P\left\{ m|n,p \right\}=\left[ \frac{n!}{m!\left( n-m \right)!} \right]{{p}^{m}}{{\left( 1-p \right)}^{\left( n-m \right)}} \qquad(4.30)\]
读为给定 \(n\) 次试验中 \(m\) 个事件为真的概率(如 \(n\) 个观测样本中出现 \(m\) 个标记),其中 \(p\) 是事件为真的概率。项 \((1-p)\) 常写作 \(q\),即 \((1-p) =q\)。 “!”符号表示阶乘。方括号中的项是组合数,是从 \(n\) 个元素中一次取 \(m\) 个元素形成的组合数,有时写成:
\[ \left( \begin{matrix} n \\ m \\ \end{matrix} \right)=\frac{n!}{m!\left( n-m \right)!} \qquad(4.31)\]
总有 \(n \geq m\) 的情况,因为一个人不可能有比试验更多的成功。
4.8.1 二项式似然的示例
作为第一个示例子,我们可以从一个种群中只捕捞雄性(澳大利亚昆士兰州捕捞泥蟹(Scylla serrata)就是一个例子)。人们可能会问,这种管理策略是否会对特定种群中合法规格动物的性别比例产生负面影响。在一个假设的 \(60\) 只动物样本中,如果我们获得了 \(40\) 只雌性动物,而只有 \(20\) 只雄性动物,那么我们是否可以得出结论,渔业对性别比例产生了影响?回答这个问题的一种方法是研究出现这种结果的相对似然(虽然二项式似然是真正的概率,但我们仍将其称为似然)。典型的性别比为 \(1:1\),这意味着我们可能会期望从 \(60\) 个样本中找到 \(30\) 只雄性动物,因此,如果我们在本例中宣布找到一只雄性动物是成功的,我们就应该研究不同 \(m\) 值的似然( \(n\) 个样本中雄性个体数),并确定在样本中找到 \(m=20\) 的相对似然。
代码
#Use Binomial distribution to test biased sex-ratio Fig 4.15
n <- 60 # a sample of 60 animals
p <- 0.5 # assume a sex-ration of 1:1
m <- 1:60 # how likely is each of the 60 possibilites?
binom <- dbinom(m,n,p) # get individual likelihoods
cumbin <- pbinom(m,n,p) # get cumulative distribution
plot1(m,binom,type="h",xlab="Number of Males",ylab="Probability")
abline(v=which.closest(0.025,cumbin),col=2,lwd=2) # lower 95% CI 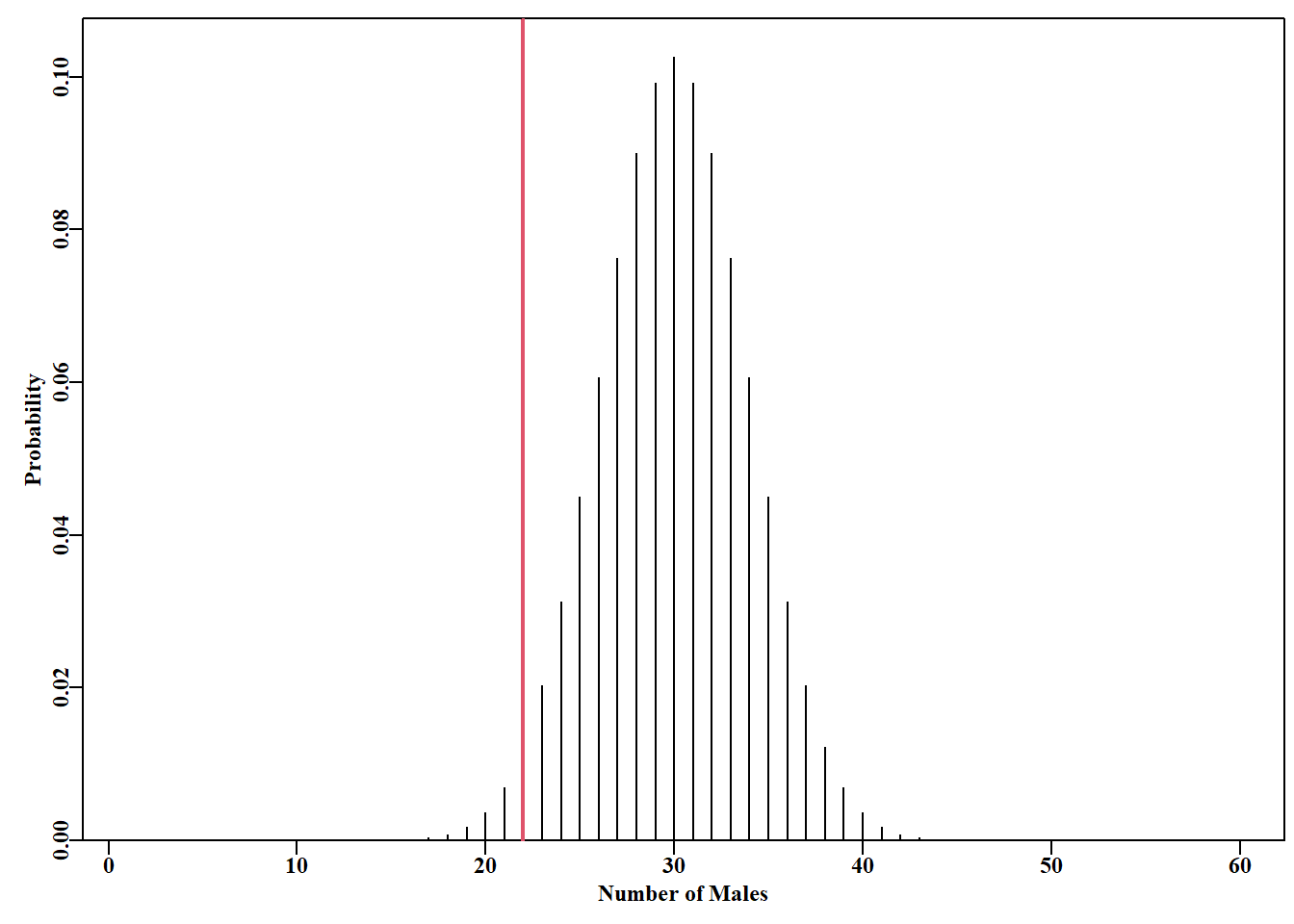
我们可以通过检查 binom(单个似然)和 cumbin(累积二项式似然)的内容来研究具体值。但很明显,如果性别比为 \(1:1\),那么获得少于 \(18\) 或多于 \(42\) 的可能性都非常小。事实上,只有 \(20\) 个雄性的可能性不到 95%。通过研究 binom[20],我们可以看到,得到整整 \(20\) 个雄性(假设性别比为 1:1)的似然刚刚超过 \(1%\) 的三分之一(\(0.003636\)),而 cumbin[20] 告诉我们,得到 \(20\) 个或更少的概率只有 \(0.006745\))。我们当然有理由说,从这一群中抽取样本的性别比率出现了下降。我们还在累积概率约为 \(0.025\) 的地方划了一条垂直线。由于我们对上限并不感兴趣,我们可以使用 \(0.05\),这样会更保守一些。但是,这种上限具有任意性,真正重要的是,捕鱼对性别比率没有重要影响的证据权重是多少?
请注意,当样本相对较大时,二项分布会变得对称。不过,尾部比正态分布窄。对于较小的样本,尤其是低 \(p\) 值,二项分布可能会高度倾斜,零成功率值具有特定的概率。
与其确定一个给定的性别比例是否合理,我们可以寻找使 \(60\) 个样本中有 \(20\) 个雄性的似然最大化的性别比例( \(p\) 值)。我们期望它是 \(20/60(0.333…)\),但仍然有兴趣知道合理值的范围。
代码
# plot relative likelihood of different p values Fig 4.16
n <- 60 # sample size; should really plot points as each independent
m <- 20 # number of successes = finding a male
p <- seq(0.1,0.6,0.001) #range of probability we find a male
lik <- dbinom(m,n,p) # R function for binomial likelihoods
plot1(p,lik,type="l",xlab="Prob. of 20 Males",ylab="Prob.")
abline(v=p[which.max(lik)],col=2,lwd=2) # try "p" instead of "l" 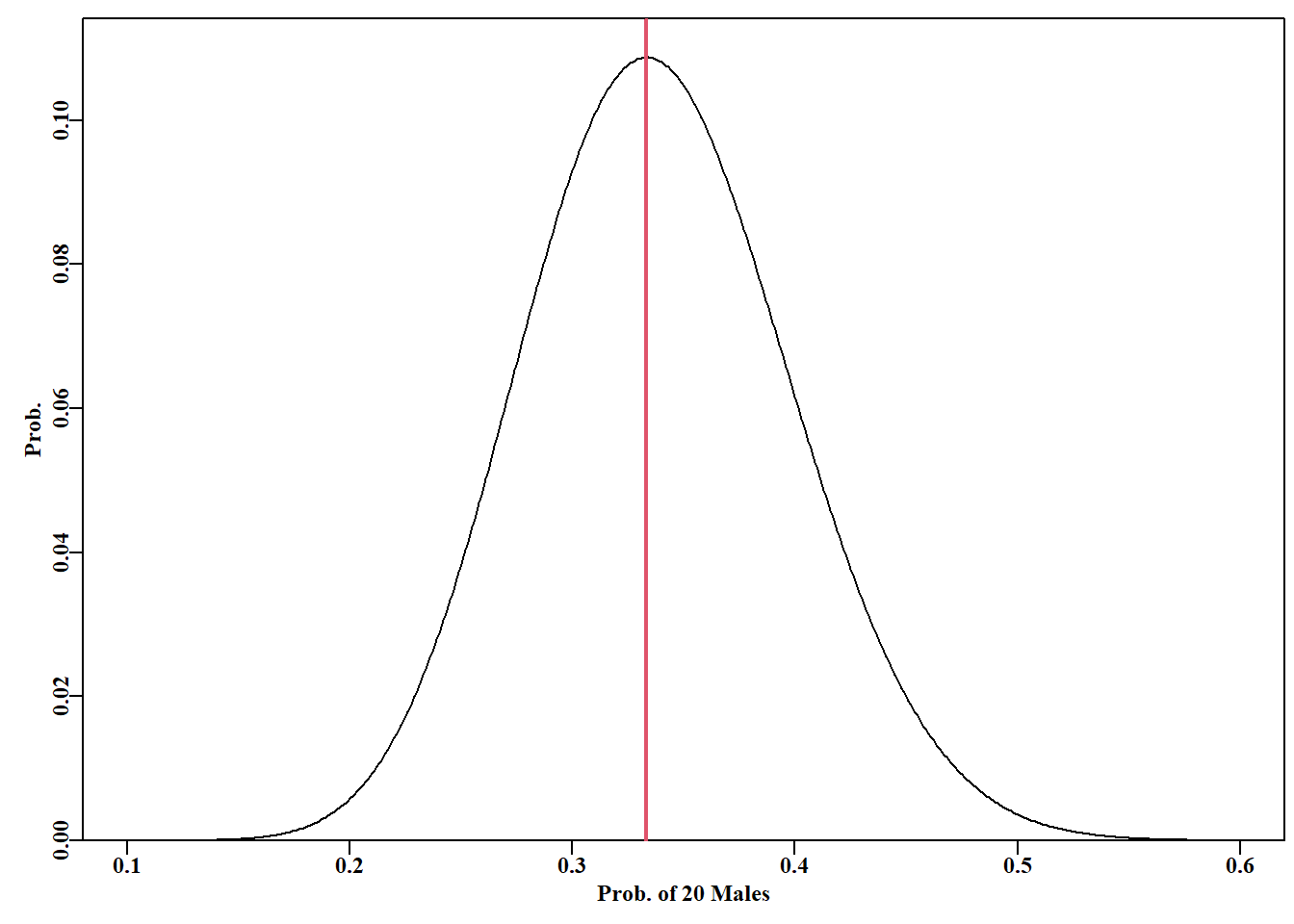
当我们只搜索一个参数时,使用 optimize()(或 optimise(),查看 ?optimize)比使用 nlm() 更有效。它需要一个函数,该函数的第一个项是要在定义的区间内最小化或最大化的值,在本例中为 \(p\),定义的区间内最小化或最大化的值,因此 dbinom() 使用了简单的封装函数。
4.8.2 开放海湾幼年海狗种群数量
与其使用第二个假设的例子,不如使用一个真实案例的数据更有意思。对新西兰南岛西海岸开阔湾群岛上的新西兰海狗(Arctocephalus forsteri)幼崽种群进行了适当的研究(Greaves,1992 ;York 和 Kozlof,1987 )。新西兰海狗在 19 世纪被大量捕杀后一直在恢复,目前在南岛和北岛都发现了新的出没地点。1894 年,新西兰正式停止了对毛皮海豹的捕猎,1978 年开始在新西兰专属经济区内对其进行全面保护(Greaves,1992 )。格里夫斯女士与新西兰保护部合作,前往其中一个近海岛屿,并在岛上度过了一周的时间。她剪掉了 151 只海狗幼崽头上的一小块护毛,给它们做了标记,然后对海狗群进行了多次巡视,以重新观察被标记的海狗(Greaves,1992 )。每次巡视都是进一步的抽样调查,每次抽样调查都发现了不同数量的被标记动物。问题是:海狗幼崽种群的数量(\(X\))是多少?
代码
# Juvenile furseal data-set Greaves, 1992. Table 4.3
furseal <- c(32,222,1020,704,1337,161.53,31,181,859,593,1125,
135.72,29,185,936,634,1238,153.99)
columns <- c("tagged(m)","Sample(n)","Population(X)",
"95%Lower","95%Upper","StErr")
furs <- matrix(furseal,nrow=3,ncol=6,dimnames=list(NULL,columns),
byrow=TRUE) 代码
knitr::kable(furs)| tagged(m) | Sample(n) | Population(X) | 95%Lower | 95%Upper | StErr |
|---|---|---|---|---|---|
| 32 | 222 | 1020 | 704 | 1337 | 161.53 |
| 31 | 181 | 859 | 593 | 1125 | 135.72 |
| 29 | 185 | 936 | 634 | 1238 | 153.99 |
所有标记实验的常规假设均适用;即我们处理的是一个封闭种群–没有迁入或迁出,在实验期间没有自然死亡或标记死亡,没有标记丢失,标记不会影响动物的重捕概率。最后,在不同的日子里,幼崽可以四处走动,因此看到的动物都是相互独立的。格里夫斯(1992)估计了所有这些影响,并在她的分析中考虑了这些影响。在对标记进行标记和重新观察后,利用彼得森估算器找到了确定性答案(Caughley, 1977; Seber, 1982):
\[ \frac{{{n}_{1}}}{X}=\frac{m}{n} \;\;\;\;\;\; \therefore \;\;\;\;\;\; \hat{X}=\frac{{{n}_{1}}n}{m} \qquad(4.32)\]
其中 \(n_1\) 是种群中标记数量, \(n\) 是后续样本量,\(m\) 是回捕的标记数,\(\hat X\) 是估算的资源量。另一种估计方法是对第二个样本的计数进行调整,以考虑到在这种情况下我们处理的是离散事件这一事实。这就是贝利调整(Bailey’s adjustment)(Caughley,1977):
\[ \hat{X}=\frac{{{n}_{1}}\left( n+1 \right)}{m+1} \qquad(4.33)\]
相关的标准误差估计值用于使用正态近似法计算近似的 95% 置信区间,从而在使用确定性方程时得出对称的置信区间。
\[ StErr=\sqrt{\frac{n_{1}^{2}\left( n+1 \right)\left( n-m \right)}{{{\left( m+1 \right)}^{2}}\left( m+2 \right)}} \qquad(4.34)\]
这些方程可以用来证实 表 4.3 中的估计。然而,与其使用确定性方程,一个好的替代方法是使用二项概率密度函数应用最大似然来估计总体大小 \(\hat X\)。
我们只估计一个参数,\(\hat X\),即总体大小,这需要搜索使数据的似然最大化的总体大小。对于二项分布,\(P \{m | n, p\}\),公式 4.30 给出了在标记比例为 \(p\) 的总体中,从 \(n\) 个样本中观察到 \(m\) 个标记个体的概率(Snedecor和Cochran, 1967, 1989;Forbes et al, 2011)。标记的幼崽比例与总体大小 \(\hat X\) 和最初标记的幼崽数量( 151 只)有关。因此 \(p = 151 / \hat X\)。我们将重新分析 表 4.3 中的前两个样本。
代码
# analyse two pup counts 32 from 222, and 31 from 181, rows 1-2 in
# Table 4.3. Now set-up storage for solutions
optsol <- matrix(0,nrow=2,ncol=2,
dimnames=list(furs[1:2,2],c("p","Likelihood")))
X <- seq(525,1850,1) # range of potential population sizes
p <- 151/X #range of proportion tagged; 151 originally tagged
m <- furs[1,1] + 1 #tags observed, with Bailey's adjustment
n <- furs[1,2] + 1 # sample size with Bailey's adjustment
lik1 <- dbinom(m,n,p) # individaul likelihoods
#find best estimate with optimize to finely search an interval
#use unlist to convert the output list into a vector
#Note use of Bailey's adjustment (m+1), (n+1) Caughley, (1977)
optsol[1,] <- unlist(optimize(function(p) {dbinom(m,n,p)},p,
maximum=TRUE))
m <- furs[2,1]+1; n <- furs[2,2]+1 #repeat for sample2
lik2 <- dbinom(m,n,p)
totlik <- lik1 * lik2 #Joint likelihood of 2 vectors
optsol[2,] <- unlist(optimize(function(p) {dbinom(m,n,p)},p,
maximum=TRUE)) 我们当然可以将结果制成表格,但更清楚的是将它们绘制为每个假设总体大小的似然(在这里是概率)。然后我们可以使用变量 optsol 中的 \(p\) 列来计算每种情况下的最佳总体大小。该图的优点是,人们可以立即看到每个样本的似然曲线的重叠,并获得任何百分位数置信区间都不是对称的印象。
代码
# Compare outcome for 2 independent seal estimates Fig 4.17
# Should plot points not a line as each are independent
plot1(X,lik1,type="l",xlab="Total Pup Numbers",
ylab="Probability",maxy=0.085,lwd=2)
abline(v=X[which.max(lik1)],col=1,lwd=1)
lines(X,lik2,lwd=2,col=2,lty=3) # add line to plot
abline(v=X[which.max(lik2)],col=2,lwd=1) # add optimum
#given p = 151/X, then X = 151/p and p = optimum proportion
legend("topright",legend=round((151/optsol[,"p"])),col=c(1,2),lwd=3,
bty="n",cex=1.1,lty=c(1,3)) 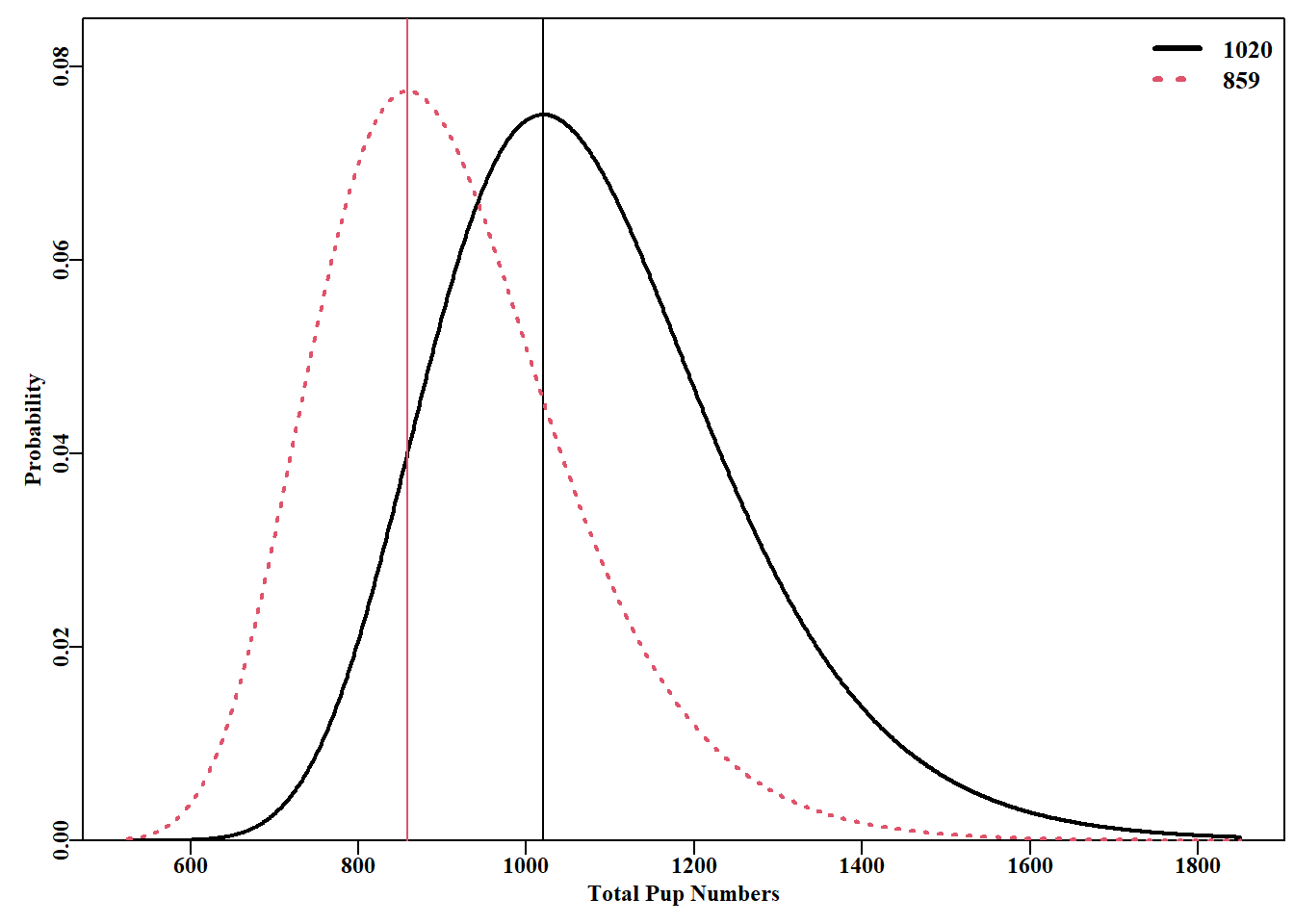
4.8.3 使用多个独立样本
如果有多个调查、观测或样本,或不同类型的数据,而这些数据又是相互独立的,那么就有可能将这些估计值合并起来,以改进总体估计值。就像概率一样,一组独立观测数据的似然是特定观测数据似然的乘积。因此,我们可以将刚才研究的两个样本的每个种群大小的似然值相乘,得到一个联合似然值,在前面的例子中,这个似然值被放入变量 totlik 中,图 4.18。
代码
#Combined likelihood from 2 independent samples Fig 4.18
totlik <- totlik/sum(totlik) # rescale so the total sums to one
cumlik <- cumsum(totlik) #approx cumulative likelihood for CI
plot1(X,totlik,type="l",lwd=2,xlab="Total Pup Numbers",
ylab="Posterior Joint Probability")
percs <- c(X[which.closest(0.025,cumlik)],X[which.max(totlik)],
X[which.closest(0.975,cumlik)])
abline(v=percs,lwd=c(1,2,1),col=c(2,1,2))
legend("topright",legend=percs,lwd=c(2,4,2),bty="n",col=c(2,1,2),
cex=1.2) # now compare with averaged count
m <- furs[3,1]; n <- furs[3,2] # likelihoods for the
lik3 <- dbinom(m,n,p) # average of six samples
lik4 <- lik3/sum(lik3) # rescale for comparison with totlik
lines(X,lik4,lwd=2,col=3,lty=2) #add 6 sample average to plot 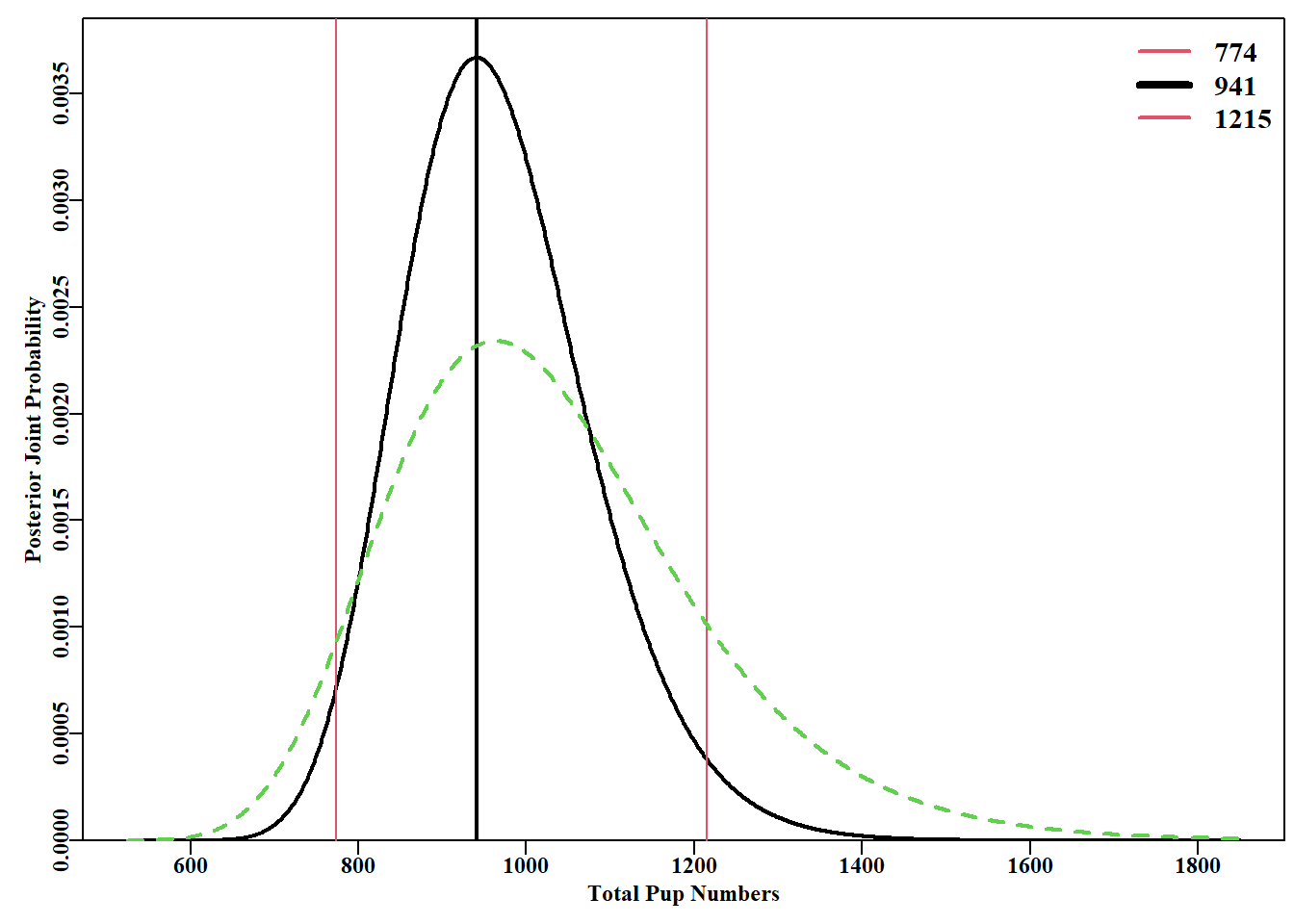
请注意,虽然中心倾向仍然非常相似,但从组合似然值(红色细线)得出的 95% 置信区间比从六个组合样本得出的平均值要小,而且在平均值周围不对称。与所有分析一样,只要使用的程序是站得住脚的,那么分析就可以继续进行(例如,在这种情况下,可以说样本是独立的,这意味着它们在时间上相隔足够远,因此无法得知被标记幼崽的位置,幼崽也可以移动等)。这与贝叶斯方法利用新数据的似然更新先验概率有相似之处。具体的贝叶斯方法将在后面详细介绍。对六个样本取平均值以获得平均计数和样本大小的方法提供了非常相似的种群估计值,但其不确定性范围更大。取这些样本的平均值并不是最佳的分析策略。
4.8.4 分析方法
有些生物过程,如动物是否成熟、是否被渔具选择捕捞等,非常适合用二项分布作为观测的基础进行分析。然而,这类过程是以累积的方式运行的,例如,随着时间的推移,种群中成熟的群体百分比最终应达到 100%。这种过程通常可以用众所周知的 logistic 曲线来很好地描述。我们可以使用数值方法来估计 logistic 模型参数,也可以使用二项分布的广义线性模型。我们将在本章之后的静态模型一章中介绍这些方法。
4.9 其它分布
在基础 stats R 软件包中(使用 sessionInfo() 确定加载的 7 个基础软件包),有许多分布的概率密度函数。事实上,只要在控制台中输入 ?Distributions(不带括号),就能立即获得 R 中可用的分布列表。此外,CRAN 系统中还有一个关于分布的任务视图,网址是:https://CRAN.R-project.org/view=Distributions。该任务视图提供了详细的讨论,同时也指向了大量独立软件包,这些软件包提供了更广泛的统计分布。
在渔业科学中,有几种其他分布可以直接使用。它们都有用于计算似然的概率密度函数(以 d 开头,如 dmultinom()),而且通常都有随机数生成器(以 r 开头,如 rgamma())。如果你查看一些函数的帮助,就会明白其中的含义和概要。下面我们将详细介绍几种对渔业和生态工作更有用的随机数生成器(另见 Forbes 等,2011 )。
4.10 多项式分布的似然
如上文所述,当观测结果有两种可能结果(真/假、标记/未标记、成熟/未成熟)时,我们会使用二项分布。不过,在很多情况下,观测结果可能会有两种以上的离散结果,在这种情况下,我们可以使用多项分布。在处理长度或年龄样本内的频率分布时,就会出现这种情况;例如,随机给定一尾鱼,它的年龄可能只是众多年龄类别中的一个。在这种多变量意义上,多项式分布是二项分布的扩展。多项式分布是另一种离散分布,它提供的是不同的概率,而不仅仅是似然。
对于二项分布,我们使用 \(P (m|n, P)\) 来表示似然。对于多项式,这需要扩展,这样就不是只有两个结果(一个概率 \(p\) ),而是在 \(n\) 个观测值的样本中,我们有 \(k\) 个可能结果中的每一个的概率( \(k_p\) )。多项式分布的概率密度函数为(Forbes et al ., 2011):
\[ P\left\{ {{x}_{i}}|n,{{p}_{1}},{{p}_{2}},...,{{p}_{k}} \right\}=n!\prod\limits_{i=1}^{k}{\frac{\hat{p}_{i}^{{{x}_{i}}}}{x!}} \qquad(4.35)\]
其中 \(x_i\) 是 \(n\) 个样本中 \(i\) 类事件发生的次数(在统计文献中通常称为试验),\(p_i\) 是 \(k\) 类可能事件中每种事件的单独概率。每种事件类型的期望为 \(E(x_i) = np_i\),其中 \(n\) 为样本量,\(p_i\) 为事件类型 \(i\) 的概率。由于 PDF 中存在阶乘项,这可能导致数值溢出问题,因此进行对数转换:
\[ \begin{aligned} P\{x_i|n,p_1, \cdots, p_k\} &=n! \prod_{i=1}^{k} \dfrac{\hat p_i^{x_i}}{x_i !} \\ LL\left\{ {{x}_{i}}|n,{{p}_{1}},...,{{p}_{k}} \right\}&=\sum\limits_{j=1}^{n}{\log\left( j \right)}+\sum\limits_{i=1}^{k}{\left[ {{x}_{i}}\log\left( {{{\hat{p}}}_{i}} \right)-\sum\limits_{j=1}^{x}{\log\left( j \right)} \right]} \end{aligned} \qquad(4.36)\]
实际上,对数变换后的阶乘项 \(n!\) 还有 \(x!\),涉及 \(\log(j)\) 的和,其中 \(j\)从 \(1\) 到 \(n\), \(1\) 到 \(x\) 的步长总是常数,通常在计算中被省略,此外负对数似然在最小化中使用:
\[ -LL\left\{{x_i}|n,{p_1},{p_2},...,{p_k} \right\} \;\;= \;\; -\sum\limits_{i=1}^{k}{\left[ {x_i}\log\left( {{\hat{p}}_{i}} \right)\right]} \qquad(4.37)\]
我们有理由费心研究概率密度函数的简化方法,因为 R 中已经开发出了非常适用于计算概率密度函数的函数。了解我们所使用的任何函数的作用始终是个好主意,这也是了解我们希望在分析中使用的任何统计函数的属性的明智之举。在某些情况下,例如 R 的 dmultinom() 用于多项式分布,它的帮助页面告诉我们,它目前还没有矢量化,因此在渔业中的使用有点笨拙。相反,我们将在 MQMF 函数 mnnegLL() 中对 公式 4.37 进行 R 运行。此外,在只处理几百个观测值时,计算速度的差异并不重要,但如果要重复计算一组数据的总对数似然几百万次(在渔业模型中使用马尔可夫链-蒙特-卡洛或 MCMC(有时为 McMC)时很有可能出现这种情况),那么任何节省时间的方法都是有价值的。我们将在讨论贝叶斯方法和其他方法来描述模型和数据中固有的不确定性时讨论这些问题。
4.10.1 使用多项式分布
在对年龄或大小组成数据进行模型拟合时,通常使用多项式分布来表示观测结果在可能类别中的预期分布。我们将以塔斯马尼亚德文特河口希望岛的黑唇鲍(Haliotis rubra)幼体的生长模态分析研究为例(Helidoniotis 和 Haddon,2012)。在 1992 年 11 月采集的样本中,以 2 毫米组距绘图时两个模式非常明显。
代码
#plot counts x shell-length of 2 cohorts Figure 4.19
cw <- 2 # 2 mm size classes, of which mids are the centers
mids <- seq(8,54,cw) #each size class = 2 mm as in 7-9, 9-11, ...
obs <- c(0,0,6,12,35,40,29,23,13,7,10,14,11,16,11,11,9,8,5,2,0,0,0,0)
# data from (Helidoniotis and Haddon, 2012)
dat <- as.matrix(cbind(mids,obs)) #xy matrix needed by inthist
parset() #set up par declaration then use an MQMF function
inthist(dat,col=2,border=3,width=1.8, #histogram of integers
xlabel="Shell Length mm",ylabel="Frequency",xmin=7,xmax=55) 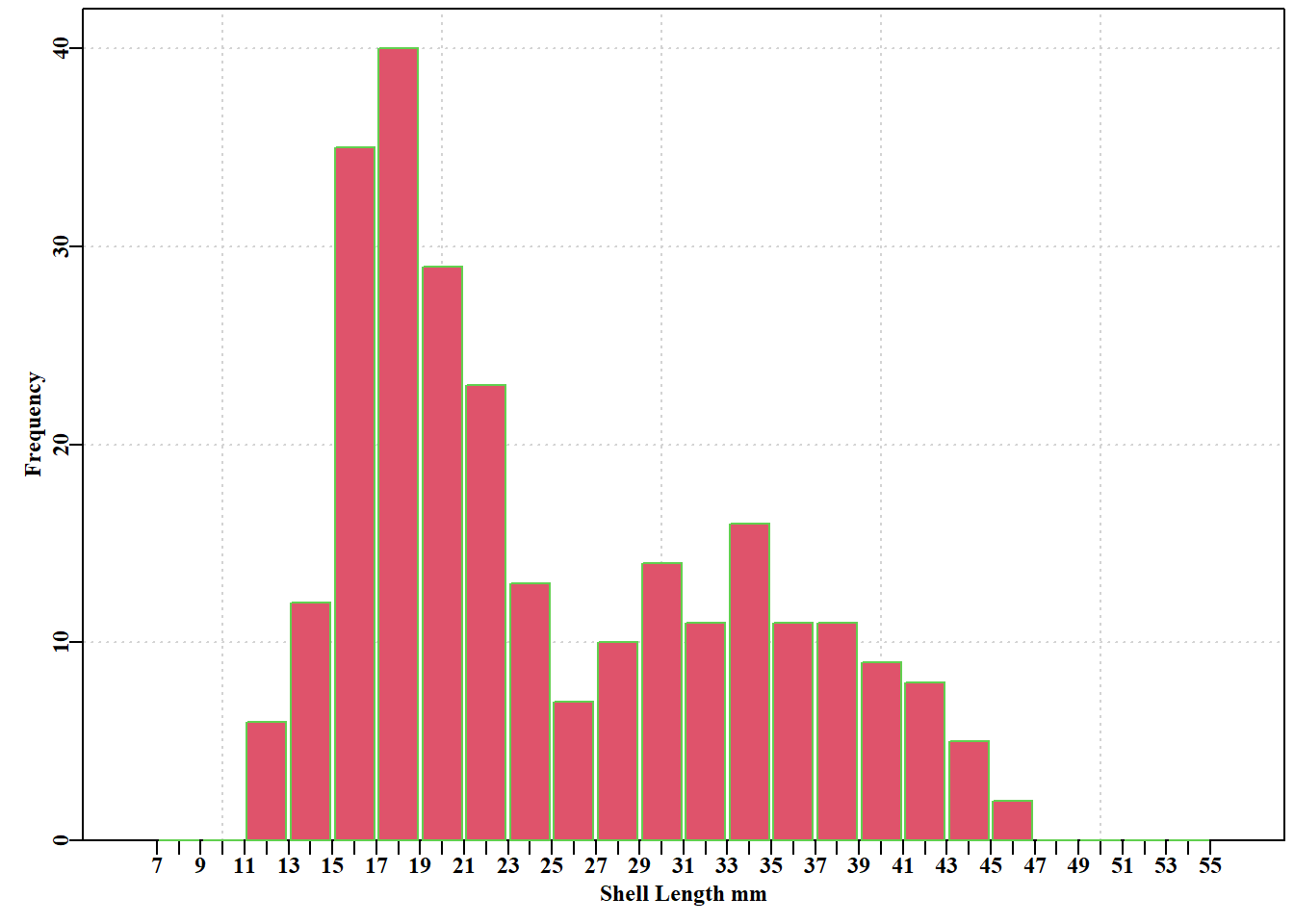
假设数据中的可观测模式与不同的世代或栖息地有关,并且我们希望估计每个世代的属性。使用正态概率密度函数来描述每种模式/队列中每个大小组的预期相对频率,并将其组合起来生成样本中 \(k\) 个 2mm 长度组中每一个的期望相对频率(Helidoniotis和Haddon, 2012)。需要五个参数,每个世代的均值和标准差,以及第一个世代中包含的观测总数的比例(第二个世代的比例是通过减去1.0得到的)。因此,使用 \(\theta=(\mu_c, \sigma_c, \varphi)\),其中,在这种情况下,有 \(c=2\) 个世代,我们可以得到每个大小分组内观测值的期望比例。一种方法是计算每个 2mm 分组中心的相对似然,乘以样本总数,再根据分配给每个世代的比例进行调节公式 4.38。
\[ \begin{aligned} {{{\hat{N}}}_{i}} &= {{\varphi }_{1}}n\sum\limits_{{{S}_{i}}=6}^{56}{\frac{1}{{{\sigma }_{1}}\sqrt{2\pi }}}\exp \left( \frac{-\left( {{S}_{i}}-{{\mu }_{1}} \right)}{2{{\sigma }_{1}}} \right) \\ &+ \left( 1-{{\varphi }_{2}} \right)n\sum\limits_{{{S}_{i}}=6}^{56}{\frac{1}{{{\sigma }_{2}}\sqrt{2\pi }}}\exp \left( \frac{-\left( {{S}_{i}}-{{\mu }_{2}} \right)}{2{{\sigma }_{2}}} \right) \\ {{p}_{i}} &= {{{\hat{N}}}_{i}}/\sum{{{{\hat{N}}}_{i}}} \\ \end{aligned} \qquad(4.38)\]
其中 \(\hat N_i\) 是每个分组 \(i\) 中观测的期望数,\(i\) 表示分组数(这晨在7-55mm 之间为 2mm 的步长,中心值为 \(8, \cdots, 54\))。\(\varphi (phi)\) 是世代 1 中发现的观测总数 \(n\) 的比例,\(\mu_c\) 为每个世代 \(c\) 的平均大小,\(\sigma_c\) 为它们的标准差。 公式 4.38 最后一行的 \(p_i\) 是分组 \(i\) 中观测值的期望比例,其中 \(S_i\) 是每个分组的中点。
或者,更准确地说,我们可以从每个大小类的顶部的累积概率中减去每个大小类i的底部的累积概率。然而,一般来说,这在分析中几乎没有什么不同,所以这里我们将只关注第一种方法(您可以尝试自己实现替代方法来进行比较,因为有时相信打印出来的一切并不是一个好主意!)。
无论采用哪种方法,我们都需要定义两个正态分布,并求和它们的相对贡献。我们可以使用对数正态分布或伽马分布等其他累积统计分布来代替正态分布。如果没有令人信服的理由来证明使用其中一种分布是正确的,那么理想的做法是比较使用其他分布与现有数据的相对拟合程度。
为了获得预期频率与观测频率进行比较,有必要限制预期总数与观测总数大致相同。多项式的负对数似然值为
\[ -LL\left\{ N|{\mu_c},{\sigma_c},{\varphi} \right\}=-\sum\limits_{c=1}^{2}\sum\limits_{i=1}^{k}{{N_i}\log\left( {{\hat{p}}_i} \right)}=-\sum\limits_{i=1}^{k}{{N_i}\log\left( \frac{{{\hat{N}}_i}}{\sum{{{\hat{N}}_i}}} \right)} \qquad(4.39)\]
其中,\(\mu_c\) 和 \(\sigma_c\) 是 \(c\) 世代假设生成观察分布的均值和标准差。有 \(k\) 个分组和 2 个世代 \(c\),\(N_i\) 是分组 \(i\) 的观测频率, \(\hat p_i\) 是组合分布分组 \(i\) 内期望比例。 目标是最小化负对数似然,以找到 \(c\) 个正态分布参数和 \(\varphi\) 的最佳组合。
代码
#cohort data with 2 guess-timated normal curves Fig 4.20
parset() # set up the required par declaration
inthist(dat,col=0,border=8,width=1.8,xlabel="Shell Length mm",
ylabel="Frequency",xmin=7,xmax=55,lwd=2) # MQMF function
#Guess normal parameters and plot those curves on histogram
av <- c(18.0,34.5) # the initial trial and error means and
stdev <- c(2.75,5.75) # their standard deviations
prop1 <- 0.55 # proportion of observations in cohort 1
n <- sum(obs) #262 observations, now calculate expected counts
cohort1 <- (n*prop1*cw)*dnorm(mids,av[1],stdev[1]) # for each
cohort2 <- (n*(1-prop1)*cw)*dnorm(mids,av[2],stdev[2])# cohort
#(n*prop1*cw) scales likelihoods to suit the 2mm class width
lines(mids,cohort1,lwd=2,col=1)
lines(mids,cohort2,lwd=2,col=4) 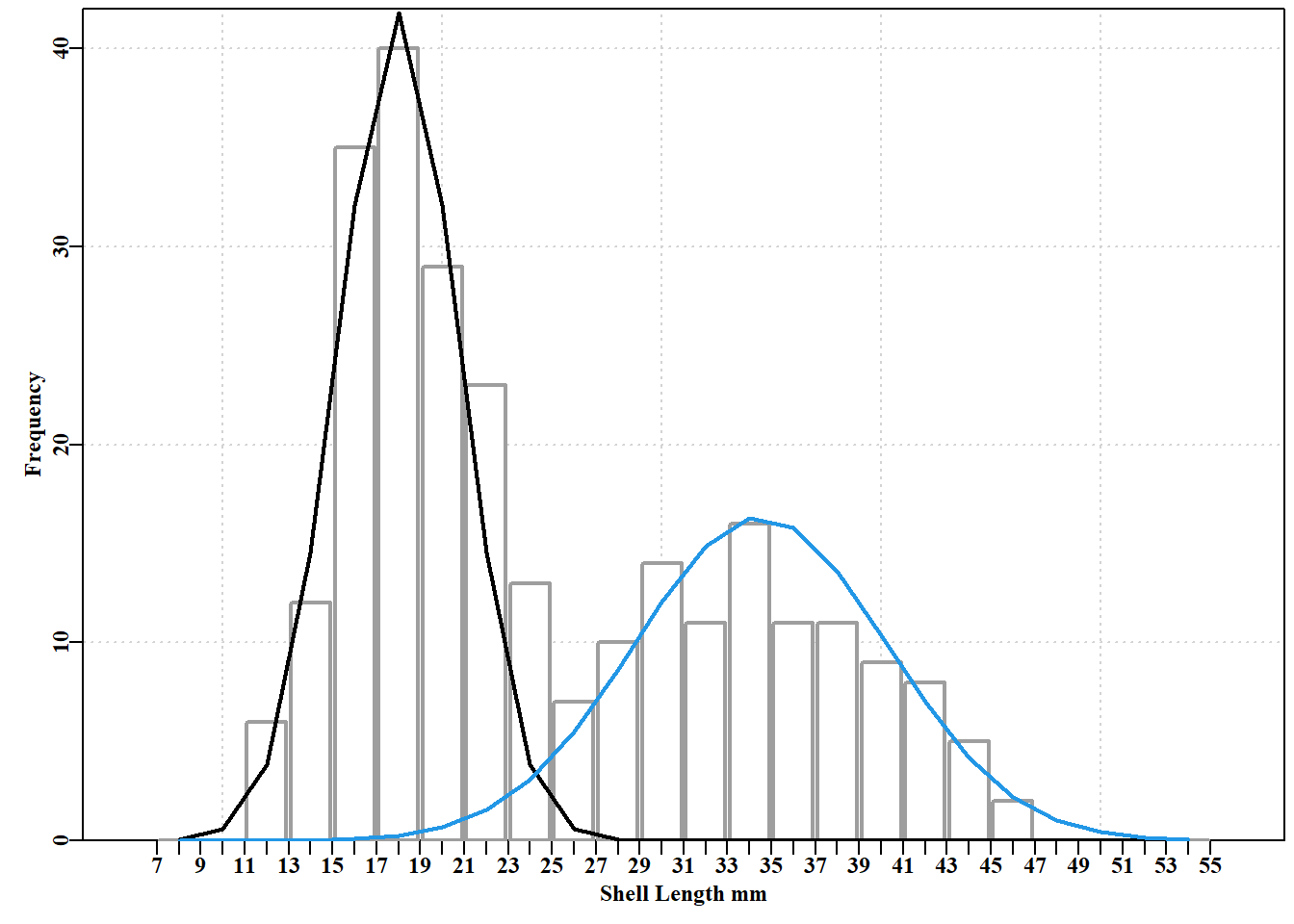
两种模式的初始试验和误差猜测的中心估计值似乎是合理的,但左侧世代中的散布似乎太小,世代间的比例分配似乎偏向于第一个世代。由于比例会以非线性方式改变数值,因此寻找最佳似然值对起始值很敏感。我们可以将 nlm() 应用于一个封装函数来生成多项式的负对数似然估计值,从而寻找一个更理想的参数集,就象 公式 4.39 中定义的那样。如前所述,我们需要一个函数来生成每个大小分组中观测值的预测数,在 MQMF 中我们称之为 predfreq()。我们还需要一个封装函数来计算使用 predfreq() 函数的负对数似然,这里我们将其称为 wrapper()(见下面的代码块)。在开发 predfreq() 函数时,我们要求对参数进行排序,首先是拟合的各世代的均值,然后是标准差,最后是分配给除最后一世代之外的所有世代的比例。这样,算法就能在规定的位置找到所需的参数。因此,对于三个世代的问题来说, 在 R 语言中,我们将有 \(pars={c(\mu_1,\mu_2,\mu_3,\sigma_1,\sigma_2,\sigma_3,\varphi_1,\varphi2)}\)。我们还加入了使用累积正态概率密度的选项。
代码
#wrapper function for calculating the multinomial log-likelihoods
#using predfreq and mnnegLL, Use ? and examine their code
wrapper <- function(pars,obs,sizecl,midval=TRUE) {
freqf <- predfreq(pars,sum(obs),sizecl=sizecl,midval=midval)
return(mnnegLL(obs,freqf))
} # end of wrapper which uses MQMF::predfreq and MQMF::mnnegLL
mids <- seq(8,54,2) # each size class = 2 mm as in 7-9, 9-11, ...
av <- c(18.0,34.5) # the trial and error means and
stdev <- c(2.95,5.75) # standard deviations
phi1 <- 0.55 # proportion of observations in cohort 1
pars <-c(av,stdev,phi1) # combine parameters into a vector
wrapper(pars,obs=obs,sizecl=mids) # calculate total -veLL [1] 708.3876代码
nlm solution: Using Midpts
minimum : 706.1841
iterations : 27
code : 1 gradient close to 0, probably solution
par gradient
1 18.3300619 6.369667e-06
2 33.7907454 4.467972e-06
3 3.0390094 -2.839356e-05
4 6.0306017 6.993965e-06
5 0.5763628 7.495453e-05代码
#Now use the size class bounds and cumulative distribution
#more sensitive to starting values, so use best pars from midpoints
X <- seq((mids[1]-cw/2),(tail(mids,1)+cw/2),cw)
bestmodb <- nlm(f=wrapper,p=bestmod$estimate,obs=obs,sizecl=X,
midval=FALSE,typsize=magnitude(pars))
outfit(bestmodb,backtran=FALSE,title="Using size-class bounds") nlm solution: Using size-class bounds
minimum : 706.1815
iterations : 24
code : 1 gradient close to 0, probably solution
par gradient
1 18.3299573 2.356852e-06
2 33.7903327 -4.690083e-06
3 2.9831560 2.221789e-05
4 6.0030194 -2.882406e-05
5 0.5763426 -5.168099e-05现在对照原始数据绘制这些最优解。绘制数据图非常简单,但随后我们需要找出每种情况下的最优参数,并计算出每个参数的隐含正态分布。
代码
#prepare the predicted Normal distribution curves
pars <- bestmod$estimate # best estimate using mid-points
cohort1 <- (n*pars[5]*cw)*dnorm(mids,pars[1],pars[3])
cohort2 <- (n*(1-pars[5])*cw)*dnorm(mids,pars[2],pars[4])
parsb <- bestmodb$estimate # best estimate with bounds
nedge <- length(mids) + 1 # one extra estimate
cump1 <- (n*pars[5])*pnorm(X,pars[1],pars[3])#no need to rescale
cohort1b <- (cump1[2:nedge] - cump1[1:(nedge-1)])
cump2 <- (n*(1-pars[5]))*pnorm(X,pars[2],pars[4]) # cohort 2
cohort2b <- (cump2[2:nedge] - cump2[1:(nedge-1)]) 代码
#plot the alternate model fits to cohorts Fig 4.21
parset() # set up required par declaration; then plot curves
pick <- which(mids < 28)
inthist(dat[pick,],col=0,border=8,width=1.8,xmin=5,xmax=28,
xlabel="Shell Length mm",ylabel="Frequency",lwd=3)
lines(mids,cohort1,lwd=3,col=1,lty=2) # have used setpalette("R4")
lines(mids,cohort1b,lwd=2,col=4) # add the bounded results
label <- c("midpoints","bounds") # very minor differences
legend("topleft",legend=label,lwd=3,col=c(1,4),bty="n",
cex=1.2,lty=c(2,1)) 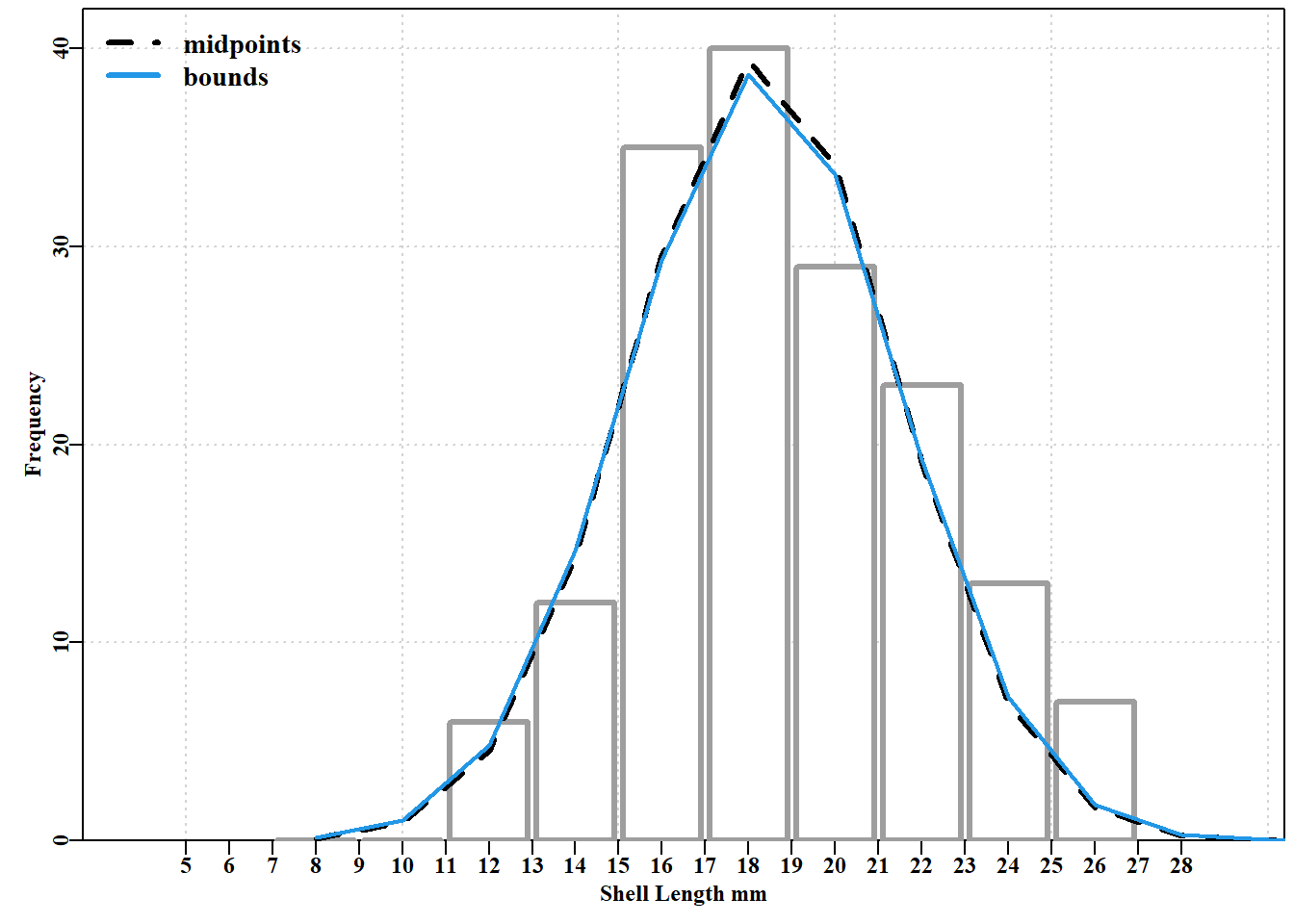
在这种情况下,使用不同长度组的中点所得到的参数与使用每个长度组的上限和下限所得到的参数几乎没有差别,所得到的正态曲线几乎完全重合。我们可以通过列出每种情况下的观测计数和预测计数,以及每个长度组中预测数和观测数之间的差异来了解这些拟合的细节。如 图 4.21 所示, 表 4.4 中的数字本身更清楚地说明了两种方法的接近性。从严格意义上讲,使用上下限更为正确,但在实践中往往差别不大。
Venebles 和 Ripley(2002,p 436)采用不同的策略将模态分布拟合为混合分布。他们的方法更为复杂和优雅,因为他们使用了分析梯度来辅助模型拟合过程。希望大家都能清楚地认识到,几乎所有分析问题都有不止一种解决方法。使用数值方法往往需要探索其他方法来寻找解决方案。
代码
# setup table of results for comparison of fitting strategies
predmid <- rowSums(cbind(cohort1,cohort2))
predbnd <- rowSums(cbind(cohort1b,cohort2b))
result <- as.matrix(cbind(mids,obs,predmid,predbnd,predbnd-predmid))
colnames(result) <- c("mids","Obs","Predmid","Predbnd","Difference")
result <- rbind(result,c(NA,colSums(result,na.rm=TRUE)[2:5])) 代码
knitr::kable(result)| mids | Obs | Predmid | Predbnd | Difference |
|---|---|---|---|---|
| 8 | 0 | 0.1243773 | 0.1487018 | 0.0243245 |
| 10 | 0 | 0.9323332 | 1.0428918 | 0.1105586 |
| 12 | 6 | 4.5513306 | 4.8235655 | 0.2722349 |
| 14 | 12 | 14.4343959 | 14.6974970 | 0.2631010 |
| 16 | 35 | 29.7390161 | 29.5254720 | -0.2135441 |
| 18 | 40 | 39.8898972 | 39.2109794 | -0.6789178 |
| 20 | 29 | 35.1655925 | 34.7612096 | -0.4043829 |
| 22 | 23 | 21.2937759 | 21.4732877 | 0.1795118 |
| 24 | 13 | 10.8867799 | 11.2235972 | 0.3368173 |
| 26 | 7 | 8.0156286 | 8.1948201 | 0.1791915 |
| 28 | 10 | 9.5119745 | 9.5509907 | 0.0390161 |
| 30 | 14 | 12.0773614 | 12.0505122 | -0.0268492 |
| 32 | 11 | 14.0532683 | 13.9953724 | -0.0578959 |
| 34 | 16 | 14.6762590 | 14.6093929 | -0.0668661 |
| 36 | 11 | 13.7319605 | 13.6776679 | -0.0542926 |
| 38 | 11 | 11.5102599 | 11.4832323 | -0.0270277 |
| 40 | 9 | 8.6431354 | 8.6453958 | 0.0022604 |
| 42 | 8 | 5.8142145 | 5.8367730 | 0.0225585 |
| 44 | 5 | 3.5038405 | 3.5336705 | 0.0298300 |
| 46 | 2 | 1.8916081 | 1.9184137 | 0.0268057 |
| 48 | 0 | 0.9148534 | 0.9339392 | 0.0190857 |
| 50 | 0 | 0.3963743 | 0.4077103 | 0.0113361 |
| 52 | 0 | 0.1538484 | 0.1596018 | 0.0057535 |
| 54 | 0 | 0.0534951 | 0.0560238 | 0.0025287 |
| NA | 262 | 261.9655804 | 261.9607187 | -0.0048617 |
4.11 Gamma 分布的似然
与我们在前几节中所考虑的统计分布相比,Gamma 分布通常不太为人所知。然而,Gamma 分布在渔业建模和模拟中越来越常用;在基于长度的种群模型中可以找到实际的例子(Sullivan等,1990;Sullivan,1992)。Gamma分布的概率密度函数有两个参数,一个尺度参数 \(b\) ( \(b < 0\);有时使用的替代方式是 \(\lambda\),其中 \(\lambda < 1/b\)),以及一个形状参数 \(c\) (\(c>0\))。分布范围是 \(0 \leq{x} \leq{\infty}\) (即无负值)。分布的期望或均值 \(E(x)\) 与两个参数(尺度参数 \(b\) 和形状参数 \(c\))有关。因此:
\[ E{( x )}=bc \;\;\;\ \text{or} \;\;\;\ c=\frac{E{( x )}}{b} \qquad(4.40)\]
计算 Gamma 分布的单个似然的概率密度函数为(Forbes et al, 2011):
\[ L\left\{ x \vert b,c \right\}=\frac{{{\left( \frac{x}{b} \right)}^{( c-1 )}}{{e}^{\frac{-x}{b}}}}{b\Gamma (c)} \qquad(4.41)\]
其中 \(x\) 是变量值 ,\(b\) 是尺度参数, \(c\) 是形状参数, \(\Gamma(c)\) 是 \(c\) 参数的 gamma 函数。\(c\) 取整数值的情况下,分布还被称为 Erlang 分布,此时 gamma 函数(\(\Gamma(c)\))替代为阶乘 \((c-1)!\) (Forbes 等,2011):
\[ L\left\{ x|b,c \right\}=\frac{{{\left( \frac{x}{b} \right)}^{\left( c-1 \right)}}{{e}^{\frac{-x}{b}}}}{b\left( c-1 \right)!} \qquad(4.42)\]
与通常的似然计算一样,为了避免过流和欠流的计算问题,标准的做法是计算对数似然,更具体地说是负对数似然。使用对数似然总是更能规避风险:
\[ -LL\{x|b,c\}= -\left[ \left( (c-1)\log\left( \frac{x}{b} \right)-\frac{x}{b} \right) -\{\log{(b)}+ \log{\left( \Gamma \left( c \right) \right)} \} \right] \qquad(4.43)\]
对于多个观测值,这可以将它们相加而不是相乘,但仍需要计算对数 gamma 函数 \(\log(\Gamma (c))\)。幸运的是在 R 语言中可以使用 gamma() 和 lgamma() 两个函数。
Gamma 分布(不要与 gamma 函数 \(\Gamma\) 混淆)非常灵活,形状的范围从实际上的反向曲线,到右偏曲线,再到近似正态曲线。它的灵活性使其成为一个非常有用的模拟函数,图 4.22。
代码
#Illustrate different Gamma function curves Figure 4.22
X <- seq(0.0,10,0.1) #now try different shapes and scale values
dg <- dgamma(X,shape=1,scale=1)
plot1(X,dg,xlab = "Quantile","Probability Density")
lines(X,dgamma(X,shape=1.5,scale=1),lwd=2,col=2,lty=2)
lines(X,dgamma(X,shape=2,scale=1),lwd=2,col=3,lty=3)
lines(X,dgamma(X,shape=4,scale=1),lwd=2,col=4,lty=4)
legend("topright",legend=c("Shape 1","Shape 1.5","Shape 2",
"Shape 4"),lwd=3,col=c(1,2,3,4),bty="n",cex=1.25,lty=1:4)
mtext("Scale c = 1",side=3,outer=FALSE,line=-1.1,cex=1.0,font=7) 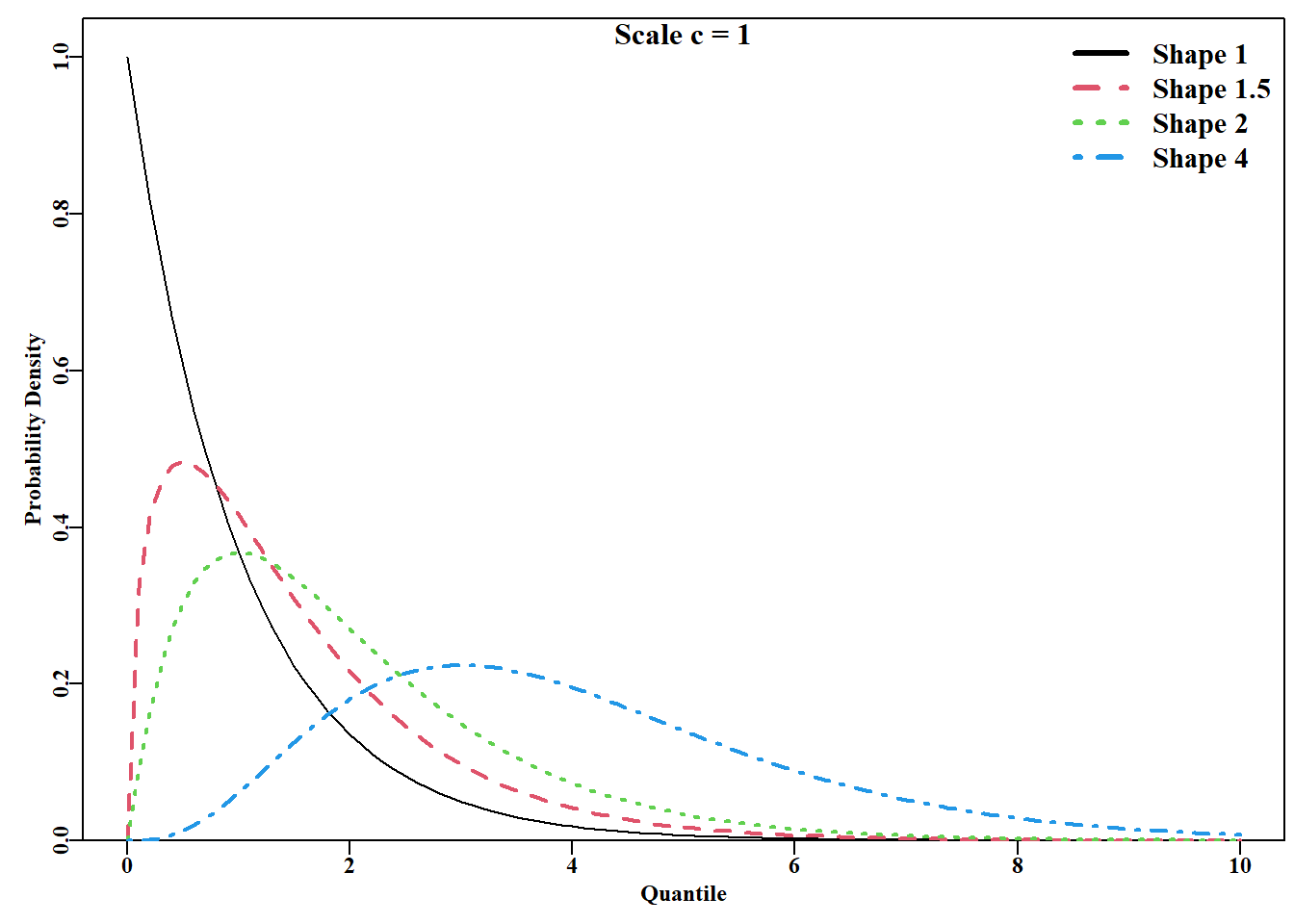
在 “多项式分布”一节中,我们使用正态分布来描述一个世代中长度的预期分布。也有可能使用 Gamma 分布来更好地描述物种的生长模式。
4.12 Beta 分布的似然
Beta 分布只适用于 0.0 到 1.0 之间的变量值。这使它成为模拟中另一个非常有用的分布,因为从 0 到 1 之间的分布中采样是比较常见的,而不可能获得超出这些限制的值,如 图 4.23 。在 “不确定性”一章中,我们将使用多变量正态分布,这需要使用一个额外的 R 软件包。可用于分析和模拟的分布阵列非常庞大。探索是发现其特性的最佳途径。
代码
#Illustrate different Beta function curves. Figure 4.23
x <- seq(0, 1, length = 1000)
parset()
plot(x,dbeta(x,shape1=3,shape2=1),type="l",lwd=2,ylim=c(0,4),
yaxs="i",panel.first=grid(), xlab="Variable 0 - 1",
ylab="Beta Probability Density - Scale1 = 3")
bval <- c(1.25,2,4,10)
for (i in 1:length(bval))
lines(x,dbeta(x,shape1=3,shape2=bval[i]),lwd=2,col=(i+1),lty=c(i+1))
legend(0.5,3.95,c(1.0,bval),col=c(1:7),lwd=2,bty="n",lty=1:5) 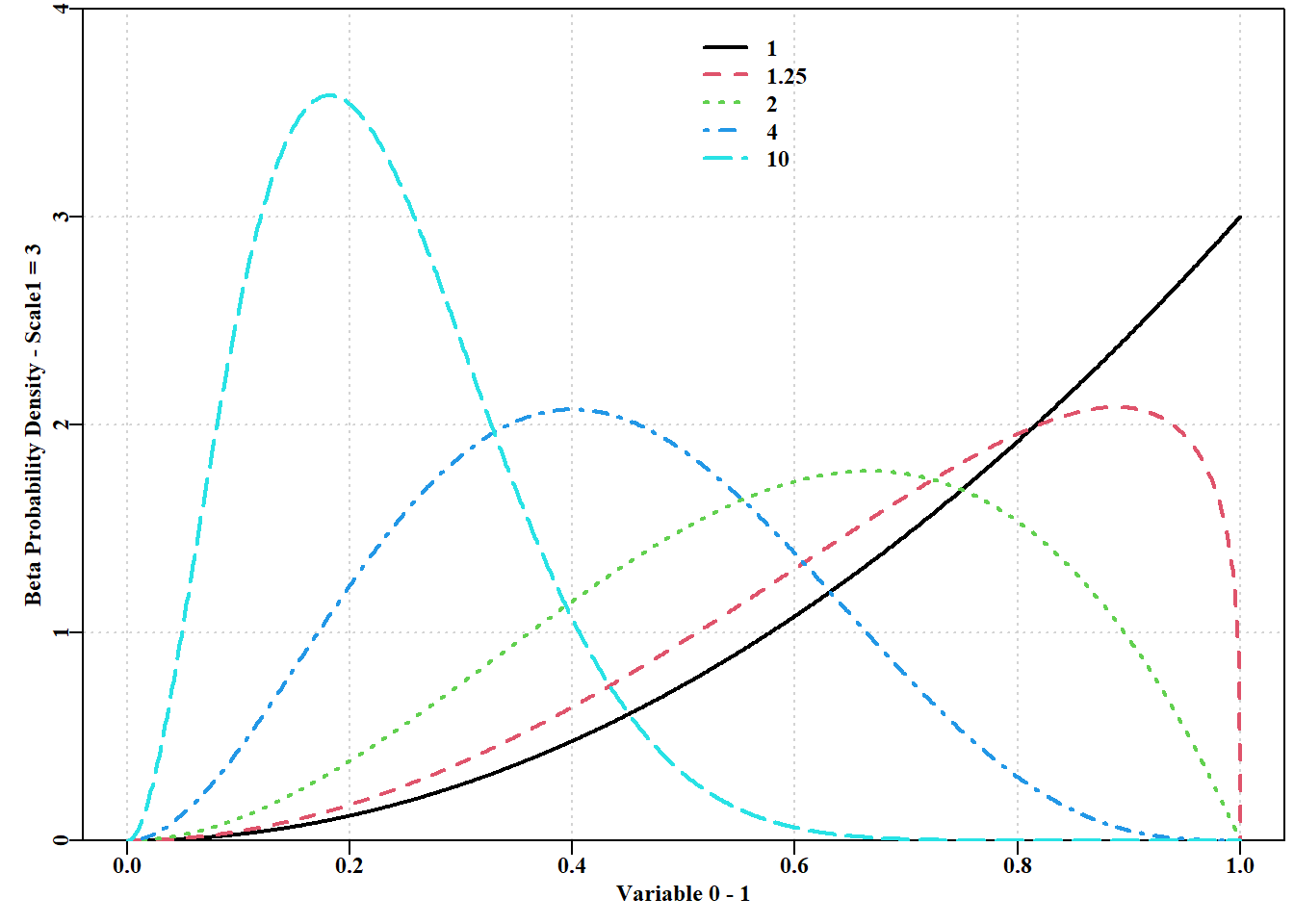
4.13 贝叶斯定理
4.13.1 简介
贝叶斯统计在渔业科学中的应用不断扩大(McAllister 等,1994;McAllister 和 Ianelli,1997;Punt 和 Hilborn,1997;反对意见见 Dennis,1996;最近见 Winker 等,2018)。Gelman 等(2014)出版了一本与这些方法的使用相关的优秀书籍。在此,我们不打算对渔业中使用的方法进行回顾;Punt 和 Hilborn(1997)中有很好的介绍,而且还有许多更近期的例子。相反,我们将集中讨论渔业中使用的贝叶斯方法的基础,并与最大似然法进行一些比较。关于如何使用这些方法的详情,请参阅 “不确定性”一章。
条件概率用于描述人们对特定事件发生的概率感兴趣的情况,比如在事件 \(A\) 已经发生的情况下,事件 \(B_i\) 发生的概率。这个表达式的符号是 \(P (B_i | A)\),其中垂直线“|” 表示“给定(given)”的意思。
贝叶斯定理就是基于对这种条件概率的操纵。因此,如果一组 \(n\) 个事件,标记为 \(B_i\),在事件 \(A\) 发生的情况下发生,那么我们可以正式地发展贝叶斯定理。首先,我们考虑在 \(A\) 发生的情况下观察到特定 \(B_i\) 的概率:
\[ P\left( {{B}_{i}}|A \right)=\frac{P\left( A \& B_i \right)}{P\left( A \right)} \qquad(4.44)\]
也就是说,在 \(A\) 已经发生的情况下,\(B_i\) 发生的概率等于 \(A\) 和 \(B_i\) 同时发生的概率除以 \(A\) 发生的概率。以同样的方式,我们可以考虑给定事件 \(B_i\) 发生的情况下事件 \(A\) 的条件概率。
\[ P\left( {A}|{B_i} \right)=\frac{P\left( {A} \& {B}_{i} \right)}{P\left( {B}_{i} \right)} \qquad(4.45)\]
这两种条件概率可以重新排列,得到:
\[ P\left( A|{B_i} \right)P\left( {B}_{i} \right)=P\left( A \& {B}_{i} \right) \qquad(4.46)\]
我们使用这个代替 公式 4.44 中的 \(P(A \& B_i)\) 项可得到 传统的贝叶斯定理:
\[ P\left({B_i}|A\right)=\frac{P\left(A|{B_i}\right)P\left({B_i}\right)}{P\left(A\right)} \qquad(4.47)\]
如果我们把这个看似晦涩的定理翻译成这样,即 \(A\) 代表从自然界获得的数据,而各种 \(B_i\) 作为可以用来解释数据的单独假设(假设是模型加上参数向量 \(\theta\)),那么我们就可以推导出渔业中使用的贝叶斯定理的形式。因此,\(P(A | B_i)\) 就是给定模型加上参数 \(B_i\) (假设)的数据 \(A\) 的似然;我们已经从极大似然理论和实践中熟悉了这一点。新内容是 \(P(B_i)\),它是在对数据 \(A\) 进行任何分析或考虑之前假设的概率。这就是假设 \(B_i\) 的先验概率。 公式 4.47 中的 \(P(A)\) 是所有可能的数据和假设组合的组合概率。“所有”这个词的使用需要强调,因为它实际上意味着考虑所有可能的结果。这种完备性就是为什么贝叶斯统计在纸牌游戏和其他受限制的机会游戏等封闭系统中如此有效的原因。然而,在开放世界中,所有的可能性都被考虑过是一个强有力的假设。最好的解释是,所考虑的一系列备选假设(模型加特定参数)构成了正在进行的分析的适用范围。b也就是对于所有 \(B_i\), \(\sum P(B_i|A)=0\),因此得到了 公式 4.48。
\[ P\left(A\right)=\sum\limits_{i=1}^{n}{P\left( A|{B_i}\right)}P\left({B_i}\right) \qquad(4.48)\]
4.13.2 贝叶斯方法
如前所述,贝叶斯定理与条件概率有关(Gelman et al, 2014),因此,当我们试图确定一系列 \(n\) 个离散假设( \(H_i = model + \theta_i\) )中哪个是最可能的时,我们使用:
\[ P\left\{ {H_i}|data \right\}=\frac{L\left\{data|{H_i}\right\}P\left\{{H_i} \right\}}{\sum\limits_{i=1}^{n}{\left[ L\left\{ data|{H_i} \right\}P\left\{{H_i}\right\} \right]}} \qquad(4.49)\]
其中 \(H_i\) 指的是被考虑的 \(n\) 个假设中的 \(i\) (假设是具有特定参数值集的特定模型),而数据只是模型拟合的数据。重要的是,\(P \{H_i | data\}\) 是假设 \(H_i\) 的后验概率(即 0 到 1 之间的严格概率)。这定义了除数 \(\sum\limits_{i=1}^{n}{\left[ L\left\{ data|{H_i} \right\}P\left\{{H_i}\right\} \right]}\),重新调整后的概率总和为 1.0。在考虑观察数据之前,\(P\{H_i \}\) 是假设的先验概率(模型加上特定的参数值)。同样,这是一个严格的概率,所有假设的先验值之和必须为 1。最后,\(L\left\{data|H_i\right\}\) 是给定假设 \(i\) 时数据的似然,正如之前在最大似然法部分所讨论的那样。
如果参数是连续变量(如von Bertalanffy 曲线中 \(L_\infty\) 和 \(K\)),替代假设必须使用连续参数的向量来描述,而不是使用离散参数集的列表,这样贝叶斯条件概率就变成了连续的:
\[ P\left\{ {H_i}|data \right\}=\frac{L\left\{ data|{H_i} \right\}P\left({H_i} \right)}{\int\limits_{i=1}^{n}{L\left[ \left\{data|{H_i}\right\}P\left\{{H_i}\right\} \right]d{H_i}}} \qquad(4.50)\]
在渔业和生态学中,要使用贝叶斯定理生成所需的后验分布,我们需要三样东西:
- 要考虑的模型假设列表(即我们要尝试的参数和模型的组合(或范围));
- 计算每个假设 \(i\) 下观测数据的概率密度所需的似然函数, \(L\left\{data|H_i\right\}\) ;
- 每个假设 \(i\) 的先验概率,标准化后所有先验概率之和等于 1.0。
除了对一组先验概率的要求之外,这与确定最大似然的要求完全相同。然而,先验概率的引入是一个很大的区别,也是我们将重点讨论的内容。这种方法的本质是利用数据信息更新先验概率。
如果模型中有许多参数需要估计,那么确定特定问题中的后验概率所涉及的整合工作就会耗费大量的计算机时间。用于确定贝叶斯后验分布的技术有很多,Gelman 等(2014)介绍了比较常用的方法。我们将介绍和讨论一种估算贝叶斯后验概率的灵活方法(MCMC),我们将在讨论不确定性特征的章节中使用这种方法。这实际上是一种新的模型拟合方法,但为了方便起见,我们将把它包含在有关不确定性的章节中。贝叶斯分析法的明确目标不仅仅是发现后验分布的模式,从最大似然的角度看,后验分布可能被认为代表了最优模型。相反,其目的是明确描述分析得出的不同可能结果的相对概率,即描述每个参数和模型输出的不确定性。可能会有一个最可能的结果,但它是在所有其他可能性的概率分布的背景下提出的。
4.13.3 先验概率
对于如何确定先验概率没有任何限制。人们可能已经从以前对同一物种的同一种群或不同种群的研究中对模型的参数有了很好的估计,或者至少对参数有了有用的限制(如不可能出现负增长或存活率 >1)。如果没有足够的信息来产生有参考价值的先验概率,通常会采用一组均匀或无信息的先验概率,即所有被考虑的假设都被赋予相等的先验概率。这样做的效果是在分析前给每个假设赋予相同的权重。当然,如果在分析中不考虑某一假设,这就等于给该假设(模型加上特定参数)分配了一个零权重或先验概率。
使用先验概率的想法之所以如此吸引人,原因之一是认为所有可能的参数值都具有同等可能性的想法有违直觉。渔业和生物学方面的任何经验都会让人对生物体的自然制约因素有先验知识。因此,举例来说,即使在彻底取样之前,就应该预料到深水(大于 800 米水深)鱼类物种,如橙连鳍鲑(Hoplostethus atlanticus),很可能寿命长、生长慢。这一特征反映了生活在低温和低生产力环境中的影响。贝叶斯方法的一大优势是,它允许人们摆脱所有可能性都具有同等可能性的反直觉假设。我们可以尝试在先验分布中捕捉模型中不同参数值的相对可能性。这样,先验知识就可以直接纳入分析。
使用先前信息可能引起争议的地方是在纳入意见时。例如,可以召集渔业利益相关者,了解他们对当前生物量等参数状况的看法(也许是相对于五年前的看法)。这种以委员会为基础的参数先验概率分布可以很容易地纳入贝叶斯分析,就像单独评估的结果一样(不是以前的评估,人们会认为以前的评估使用了大部分相同的数据,而是使用了独立的数据)。在正式分析中,是否应同样接受来自这些不同来源的先验数据,经常引起争论。Punt 和 Hilborn(1997,第 43 页)在一篇可读性很强的文章中讨论了先验来源的合理性问题:
因此,我们强烈建议,无论何时进行贝叶斯评估,都应非常谨慎地充分记录各种先验分布的依据….。在选择先验函数形式时应小心谨慎,因为选择不当会导致不正确的推论。我们还注意到一种低估不确定性的倾向,即指定不切实际的先验信息–这种倾向应得到明确承认并加以避免。
辩论的有效性的使用丰富的案底已经这样,walters 和 Ludwig (1994)建议非翔实的先验被用来作为一个默认在贝股的评估。 然而,除了不同意沃尔特斯和路德维希,平底船和Hilborn(1997年)突出强调的一个问题与我们的能力产生非翔实的前科(Box 和 Tiao,1973). 一个问题产生非翔实的先验是,他们感到特别测量系统( 图 4.24). 因此,现有概率密度,是统一的线性规模将不代表一个统一的密度在一个日志的规模。
代码
# can prior probabilities ever be uniniformative? Figure 4.24
x <- 1:1000
y <- rep(1/1000,1000)
cumy <- cumsum(y)
group <- sort(rep(c(1:50),20))
xlab <- seq(10,990,20)
par(mfrow=c(2,1),mai=c(0.45,0.3,0.05,0.05),oma=c(0.0,1.0,0.0,0.0))
par(cex=0.75, mgp=c(1.35,0.35,0), font.axis=7,font=7,font.lab=7)
yval <- tapply(y,group,sum)
plot(x,cumy,type="p",pch=16,cex=0.5,panel.first=grid(),
xlim=c(0,1000),ylim=c(0,1),ylab="",xlab="Linear Scale")
plot(log(x),cumy,type="p",pch=16,cex=0.5,panel.first=grid(),
xlim=c(0,7),xlab="Logarithmic Scale",ylab="")
mtext("Cumulative Probability",side=2,outer=TRUE,cex=0.9,font=7) 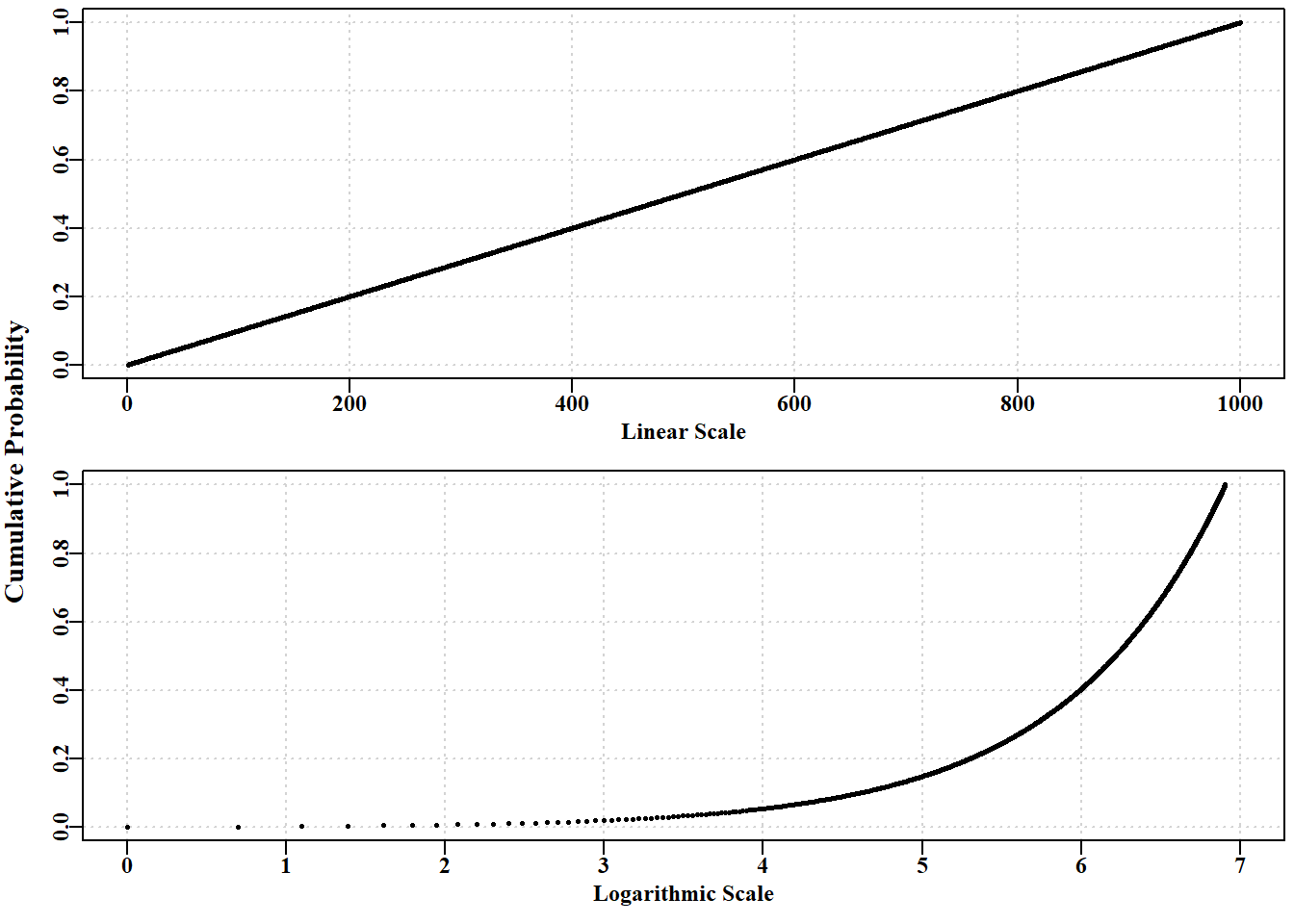
由于渔业模型往往充满非线性关系,使用非信息先验是有争议的,因为对某些参 数非信息先验很可能对其他参数有信息影响。虽然这种影响可能是无意的,但却不容忽视。这意味着信息可能以完全无意的方式被纳入模型,这也是讨论先验概率时争议的一个来源。如果要使用先验概率,那么 Punt 和 Hilborn(1997 年)关于充分记录先验概率的起源和属性的建议是非常明智的。我们将在 “不确定性”一章中更详细地探讨贝叶斯方法的使用。
4.14 结语
在任何分析情况下,使用哪种方法最合适在很大程度上取决于分析的目标。如果只想找到模型的最佳拟合方法,那么使用最小二乘法、最大似然法还是贝叶斯法其实并不重要。有时,先用最小二乘法拟合模型,然后再用似然法或贝叶斯法建立置信区间和进行风险评估,可能会更容易一些。
模型参数和输出的置信区间可以用传统的渐近方法(保证对称,对于强非线性模型,只能大致近似)、似然法或贝叶斯后验积分法(两者显然密切相关)来生成,也可以用引导法或蒙特卡洛技术。
并不是说只有使用贝叶斯方法才能更详细地评估备选管理方案的相对风险。Bootstrapping 和 Monte Carlo 方法为开展此类工作提供了必要的工具。首要问题是确定分析目标。然而,如果在拟合模型时,不对每个参数的不确定性以及模型对各种输入参数动态的敏感性有一定的了解,那将是一种糟糕的做法。由于各种方法之间没有明显的优胜者,如果有时间,使用一种以上的方法(特别是比较似然概 念、贝叶斯后验和引导法)是一个合理的想法。至于是否有足够的资源让资源建模者有时间进行这一系列分析,则是一个不同但同样现实的问题。如果发现存在重大差异,那么最好对其背后的原因进行调查。如果不同的程序得出的答案大相径庭,则可能是对现有数据的要求过高,需要进行不同的分析。